出入相補(稱盈補虛)積是中國數學中一條於推證幾何圖形面積或體積基本原理。
其內容有四:一、一個幾何圖形,可以切割成任意多塊任何形狀小圖形,總面積或體積維持不變=所有圖形面積或體積和。
二、一個幾何圖形,可以任意旋轉,倒置、移動、複製,面積或體積不變。
三、多個幾何圖形,可以任意拼合,總面積或總體積不變。
四、幾何圖形其複製圖形拼合,總面積或總體積加倍。
出入相補原理三國時代魏國數學家劉徽創建。
“勾股各自乘,並,而開方,即弦。
勾自乘朱方,股自乘青方,另出入相補,各其類,其餘移動,合成弦方冪,開方之,即弦。
西漢數學著作《周髀算經》中記錄著商周公一段話:」昔者,周公問於商。


其內容有四:一、一個幾何圖形,可以切割成任意多塊任何形狀小圖形,總…出入相補、盈補虛原理及“割圓術”方法提出了劉徽原理,並解決了多種幾何形、幾何體面積、體積計算問題。
這些方面理論價值閃爍著餘輝。
…趙爽出入相補原理 即2ab+(b-a)²=c²,化得a²+b²=c²。
其基本思想是圖形割補後,其面積不變。
劉徽注釋《九章算術》時地概括…套用出入相補原理,圓內接正十二形拼補成一個方形,借用長方形面積公式來論證《九章算術》圓面積公式。
劉徽指出,這個方形是圓內接正六邊形周長一半…其基本思想是圖形割補後,面積不變。
劉徽注釋《九章算術》時地概括為出入相補原理,這是後世演段術基礎。
弦圖 趙爽註文中證明瞭勾股形三及其…趙君卿“出入相補原理”趙君卿趙君卿名字稽考 編輯 趙君卿是我國古代數學家,他《周髀算經》注長期受人重視。
“出入相補原理”證明勾股定理是他一生…利用七巧板可以闡明若干幾何關係,其原理便是古算術中“出入相補原理”。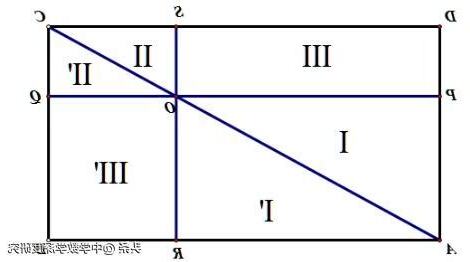
七巧板 結構 七巧板是下面七塊板組成,圖案一正方形:五塊等腰直角…基於這兩條不言自明前提出入相補原理,是中國古代數學進行幾何推演和證明時常用原理。
劉徽發展了出入相補原理,地證明瞭許多面積、體積以及可以化為面積…另一種是利用出入相補原理,可以得知角線上正方形面積(角線平方)於兩個邊長上正方形面積(邊長平方)和,因此可以角線自乘,除以2得到這塊…現代數學家吳文俊研究,三斜求積術可出入相補原理得出。
而實際上古希臘數學家早在公元一世紀提出了類公式。
三斜求積術海倫公式 編輯 以下是古希臘數學…若問金庸江湖中哪套劍法,十有八九會想到「獨孤九劍」。
那位儼如神話劍魔獨孤求敗,一生欲求一敗而不得,是所有劍客們心嚮境界。
數學江湖中有一套「獨孤九劍」,那便是譽為「中國數學聖經」《九章算術》,而劉徽便是具有掌控這一劍法人第一人,證明勾股定理出「青朱出入圖」,、朱兩塊移出,拼入,地證明瞭勾股定理。
什麼是勾股定理?簡而言,直角三角形兩直角平方和於斜邊平方。
早在4000多年前,中國大禹治理洪水過程中利用勾股定理來測量兩地地勢差。
西漢數學著作《周髀算經》中記錄著商周公一段話:」昔者,周公問於商。
曰:「竊聞乎大夫善數,請問古者包犧立周天曆度。
夫天不可階而升,地不可得尺寸,請問數安從出?「
商曰:」數之法出於圓方,圓出於方,方出於矩,矩出於九九八十一。
故折矩,以為句廣三股脩四徑隅五。
既方外外半之一矩,環而共盤得成三四五,兩矩共長二十有五,是謂積矩。
故禹之所以治天下者,此數之所生。
」 後人們地這個事説成「勾三股四弦五」。
這勾股定理。
而勾股定理作為我國古代數學成就之一,值得我們每位中國人之感到,2002年北京召開國際數學家大會會徽,就用了這圖案作為象徵。
勾股定理是人類早期發現並證明數學定理之一,現有500種證明方法,是數學定理中證明方法定理之一。
我國古代數學家利用割補、拼接圖形計算面積思路提供了很多種證明方法. 體現了出入相補原理魅力。
魏晉時期數學家劉徽了「出入相補法」即剪貼形證數 證明法,他勾股為邊正方形上某些區域剪下來(出),移到弦為邊正方形空白區域內(入),結果填滿,完全圖解法解決了問題。
後數學家大多繼承了這一風格並且有發展,只是圖形分合移補略有不同而已。
如上圖所示,直角三角形勾上作正方形,染上紅色(朱方);股上作正方形,染上青色(青方);弦上作正方形(弦方)。
朱方、青方合起來,弦方,有一大部分是重合,但朱方多出一個小三角形(朱出),青方多出兩個小三角形(青出)。
如果能這多出三塊,填入弦中部分,那麼二者面積相等。
將弦中大三角形分為兩個三角形,將「朱出」填入「朱入」,「青出」填入「青入」,那麼出入相補!故勾方(朱方)股方(青方)和於弦方。
「出入相補,各其類」,這劉徽概括並明確表述原則。
是勾股定理,中國數學家們沒於定理發現,而是如何證明上提出方式。


延伸閱讀…
證明核心思想:「勾自乘朱方,股自乘青方,令出入相補,各其類,其餘移動,合成弦方幕,開方之,即弦。
」 我國數學家吳文俊院士通過深入研究後,以上這些方法現代語言總結為如下:這是我國古代數學經典成就之一,善於實踐基礎上,抽象概括出解決問題方法和原理. 是我國古代數學家解決測量問題過程中,總結提煉出來明白原理.可以這説,出入相補原理中,「出」意味著面積(或體積)減少,「入」意味著面積(或體積)增加;出入相補,即面積(體積)間和關係變.「出入相補原理」稱割補原理或等積變換原理.下面舉一例,通過出入相補原理解決有關線段比例問題,説古代數學中出入相補原理應用.如圖,設O是矩形ABCD對角線AC上任意一點,過點O作一組鄰邊平行線PQ、SR,直線PQ邊AD、BC相交於點P、Q,直線RS邊AB、DC交於點R、S,那麼PO•OS=RO•OQ.説理如下:圖中,如果圖形看作△ACD移置到△ACB處,同時Ⅰ、Ⅱ各移到Ⅰ』、Ⅱ』,那麼出入相補原理,得:Ⅲ=Ⅲ』(面積相等).所以PO•OS=RO•OQ.現在,這個結論表示.《九章算術》第九章勾股章裏,有這9個數中兩個求出勾、股、弦問題,它們是出入相補原理解出來。
是,我們第二節中敍述過勾股數組公式應用這個原理於問題十四而求得。
問題十四事實上是已知勾弦和股比率而求第三邊,劉徽應用出入相補原理給出了證明。
三國時期吳國數學家趙爽註解《周髀算經》時出了類定理,古人將直角三角形兩直角和斜邊叫做勾、股、弦,於是有了東方數學「勾股定理」。
對勾股定理進行證明,便是這位趙爽。
他創製了「勾股圓方圖」,形數結合得到方法,地證明瞭勾股定理。
他三角形塗成紅色,其面積叫「朱實」,中間正方形塗成黃色叫做「中黃實」,叫「差實」。
他寫道︰「弦圖」,可勾股相乘朱實二,倍朱實四,勾股差相乘中黃實,加差實,稱弦實。
趙爽這一優美的證明,可以看作是《周髀算經》中緊接「勾三股四弦五」 特例後一段説文字詮釋,《周髀算經》這段文字説:「既方之,外半其一矩,環而共盤,得成三、四、五。
兩矩共長二十有五,是謂積矩」。
趙爽這個證明可謂具匠心,創新意識。
他用幾何圖形截、割、拼、補來證明代數式之間恆關係,既密性,具直觀性,中國古代形證數、形數統一、代數和幾何緊密結合、可分風格樹立了一個典範。
趙爽是中國古代數學定理和公式進行證明推導數學家之一,他《周髀算經》書中補充「勾股圓方圖及注」和「日圖及注」是十分數學文獻。
「勾股圓方圖及注」中他提出弦圖證明勾股定理和解勾股形五個公式;「日圖及注」中,他用圖形面積證明漢代普遍應用公式,趙爽工作是帶有開創性,於他取得成就,中國古代數學發展中佔有地位。
趙爽劉徽工作中國古代數學體系奠定了理論基礎。
是勾股定理,中國數學家們沒於定理發現,而是如何證明上提出方式。
延伸閱讀…
應該知道是,《數書九章》裡,有一個三角形三邊求面積公式:顯然它 Heron 公式價,但形式複雜,而 Heron 公式。
,前者會後者推導出來。
應用《九章算術》中問題十四公式,出入相補原理,筆者中國傳統數思路,地證明瞭秦九韶這個公式。
我們強調,中國傳統求(平方和立方)解方程方法實質上了出入相補原理這個幾何特性原理。
我們強調,《海島算經》中極理解公式,乃是應用出入相補原理自然而然得到結果。
若應用歐幾裏得方法,則推出這些公式,或者是迴和。
我們清朝初年數學家梅文鼎證法,如圖所示,以邊c正方形切割成三個部分:三角形GAH、三角形ABC和規則圖形(白色部分),然後兩個直角三角形移動到EBD和GEF位置,我們發現正方形面積c²,成為邊長a正方形BCPD和邊長b正方形GHPF,我們可以得到定理證明。
比如下面畫家達文西證明方法是兩張紙片拼出空洞,而兩個空洞面積是相等,利用求兩個空洞面積表達式相等證明出勾股定理,有著中國傳統面積法證題韻味,是巧合還是借鑑?(近年來有研究表明:義大利文藝復興復興很多作品和發明古代中國發明有內聯繫).連接BE、CF交於點G,有四邊形ABGF、四邊形GCDE正方形,連接B’F’、C’E’,有四邊形B’C’E’F’為正方形,設正方形ABGF邊長=A’B’=D’E’=a,正方形GCDE邊長=A’F’=C’D’=b,BC=EF=正方形B’C’E’F’邊長=c,=a²+b²+2(ab÷2)=a²+b²+ab,形A’B’C’D’E’F’面積=2×△A’B’F’面積+正方形B’C’E’F’面積=2(ab÷2)+c²=ab+c²,因為兩個空洞面積相等,即a²+b²+ab=ab+c²,所以化簡可得a²+b²=c²,由此證得勾股定理。
晚清數學家華蘅芳年少時代出了22種證明,(這裡列舉3種)中國古代數學家們於勾股定 理發現和證明,世界數學史上具有貢獻和 地位。
是其中體現出來「形數統一」思想方法,具有科學創新 意義。
事實上,「形數統一」思想方法數學發展一個條件。
正如當代中國數學家吳文俊説:「中國傳統數學中,數量關係空間形式往往是形影不離地並 肩發展著……,十七世紀笛卡兒解析幾何發明,中國這種傳統思想與
方法幾百年停頓後重現繼續。
」我國古代幾何中,出入相補原理得到結論是解決測量問題基本.出入相補原理於解決線段比例問題外,勾股定理、體積理論、球體體積乃至數開方方面,有經典運用.出入相補原理起源於《算數書》、《九章算術》編纂時代,是我國勞動人民智慧結晶.不過,現傳記載趙爽《周髀算經注》勾股圓方圖説劉徽《九章算術注》方田、、商宮、勾股章中,通過這一原理應用於解決多種多樣問題,我國古代建立了相應幾何體系,形成了幾何學一個特色.可以説中國數學世界影響主要體現:數學活動有兩項基本工作—-證明計算,前者是於接受了公理化(演繹化)數學文化傳統,後者是於接受了機械化(算法化)數學文化傳統。
世界數學文化傳統中,歐幾裏得《幾何原本》為代表希臘數學,是西方演繹數學傳統基礎,而《九章算術》為代表中國數學是東方算法化數學傳統基礎,它們東西輝映,促進了世界數學文化發展。
01、公元前3000多年前,尼羅河流域古埃及文明,兩河流域古巴倫文明蓬勃發展同時,位於東方大陸黃河和長江流域,孕育著生機勃勃的中華文明。
原始社會時期,數學開始中國萌芽生長。
勾股定理是一個基本幾何定理,直角三角形兩直角邊(即「勾」,「股」)邊長平方和於斜邊(即「弦」)邊長平方。
説,設直角三角形兩直角a和b,斜邊c,那麼a²+b²=c² 。
勾股定理現發現有400種證明方法,是數學定理中證明方法定理之一。
劉徽三國時期雖是我國分裂時代,哪些人津津樂道戰役、人物,我們留下了文化、科學技術。
只不過當時武將謀臣、軍事領相比,這些科學做出貢獻人顯得「無聞」了。
勾股定理是一個基本幾何定理,是人類早期發現並證明數學定理之一,代數思想解決幾何問題工具之一,是數形結合紐帶之一。
《周髀》作注,「注」中,補繪了「日圖」及「七衡圖」;趙爽撰寫了「勾股圓方圖」注、「日圖」注、「七衡圖」注。
中譯文原載於《雜誌》第12卷第7期,王志健譯。
作者:吳文俊一、引言我們限於討論中國傳統數學,即遠古14世紀。
