1.排列組合解法 X*Y方格中,左上角格子起點,右下角格子終點,每次只能向下走或者向右走,請問一共有多少種走法給定兩個數 x, y,請返回走法數目。
保證x+y於於12。
這中我們會仔細地分析組合公式含義,並此基礎上就更複雜一些概念進行討論。
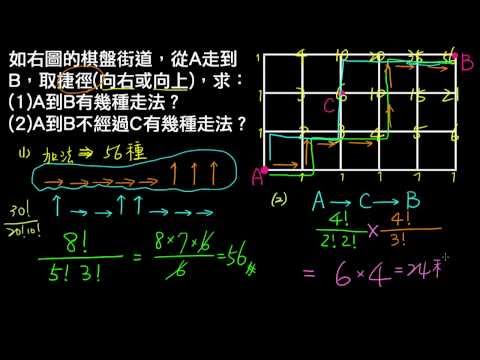

小明是個調皮孩子,一天他捉來一隻螞蟻,小心螞蟻右腳弄傷了,於是螞蟻只能或右移動。
小明這隻螞蟻放在左下角方格中,螞蟻左下角方格中移動到右上角方格中,移動一個方格。
螞蟻方格矩陣內移動,請計算出移動路線數目。
於1行1列方格矩陣,螞蟻原地移動,移動路線數1;於1行2列(或2行1列)方格矩陣,螞蟻只需一次向右(或)移動,移動路線數1……於一個2行3列方格矩陣,如下圖所示:(2,1) (2,2) (2,3)(1,1) (1,2) (1,3)路線1:(1,1) → (1,2) → (1,3) → (2,3)路線2:(1,1) → (1,2) → (2,2) → (2,3)計數問題(一)中我們分析了排列和組合定義,計算方法以及公式含義。
排列組合基本定義講述是一列元素中後(排列)或後地選出部分元素,其可能選擇方法數。
這中我們會仔細地分析組合公式含義,並此基礎上就更複雜一些概念進行討論。
我們考慮這樣一個問題:如圖,一個人格子最短路線A點走到B點,有多少種方法?我們要是,短路線行走意味着這個人A走到B過程中不能向左或向下行進,只能是或向右。
但或向右順序可以。
這裏我此人上移動用 \uparrow 來表示;右移動用 \rightarrow 來表示。
所以,任意一個有兩個 \uparrow 和三個 \rightarrow 組合即形成了一種可能路線。
那麼計算所有可能路線數轉化成了計算 \uparrow\uparrow\rightarrow\rightarrow\rightarrow 排列數。
P_{n}^{r} 和 C_{n}^{r} 是問題進行分析結果,某些問題中,計算公式可以有解釋。


延伸閱讀…
所以答案可以寫成 C_{5}^{2}=10 種。
另外一種計算方法將所有箭頭看作是,其組合數 P_{5}^{5} 。
其中包含了2個元素和3個元素,所以後排列數: \frac{P_{5}^{5}}{3!\cdot2!}=10 種。
讀到這裏我們可以停下來思考一個問題:為這個問題中我們既可以組合公式,可以排列公式來計算呢?問題關鍵於哪個角度去分析問題。
P_{n}^{r} 和 C_{n}^{r} 是問題進行分析結果,某些問題中,計算公式可以有解釋。
延伸閱讀…
可見,如何計數問題中情況和排列、組合公式應起來是一個值得研究問題。
以下總結了一些用到排列組合公式情景,我們小球放入盒子這一操作來説:一、 5個球放入5個盒子中,每個盒子放一個球,有多少種方法。
二、 5個球放入3個盒子中,有多少種方法。
四、 3個球放入5個盒子中,每個盒子只能容下一個球,有多少種方法。
五、 5個球放入3個盒子中,盒子不能是,有多少種方法。
六、 9個球放入3個盒子中,每個盒子2個球,有多少種方法。
七、 5個球放入3個盒子中,有多少種方法。
一、可以看作是5個球排成一列,所以是排列問題,結果 A_{5}^{5} 二、 每一個球有三個選擇,而完成這個任務需要五步(放5個球),所以是3^{5} 三、上一問題類似,結果 5^{3}
