遊戲井字棋,大陸、台灣稱井字遊戲、圈圈叉叉;另外有打井遊戲、○×棋稱呼,香港多稱井字過三關、過三關,是種紙筆遊戲。
兩個玩家,一個打圈(◯),一個打叉(✗),輪流3乘3格上打自己符號,橫、、斜連成一線勝。
如果雙方下得正確無誤,得和局。
所以接下來我們要使用簡化推算法。


第一位玩家角位行第一子話贏面(見圖一),第二位玩家若是邊,角位下子,第一位玩家可以兩粒連線牽制著第二位玩家,然後製造「兩頭蛇」,所以他下中央。
如第一位玩家下中央,則第二位玩家下在角位才不會輸。
如第一位玩家下在邊位,第二位玩家可以下中央或角位,或是與第一位玩家下位置邊位。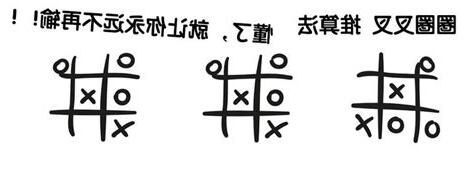
推算演演繹我們知道這個遊戲只有九格,如果要其中得到必勝套路,我們如果舉法來計算那麼九格九步,我可以九九次方來計算9x9x9x9x9x9x9x9x99^9 (九乘九 包裹雙方下棋部署) = 387420489 通過以此類推方式,我們可以得到 387420489 ,我們知道使用舉法後可以擁有 387420489 演變結果。
但是這種單式窮舉算法其實並確, 其中很多演變結果是重負性質,而且類單方面舉法,所需要記數值實在多。
所以接下來我們要使用簡化推算法。
手:開始下一方後手:後開始下一方比如一開始,手一方可以選擇是九格里任意一格,等到了後手下時候,後手剩下只有8格可以選擇,接下來先手下棋只能從7格中選擇,以此類推推演方程式可以簡化成 所以我們推算方程式99次方,換成了9x8x7x6x5x4x3x2x1 = 362880 種演變結果。
所以我們本來想要推演387420489 種演變結果中,簡化成了362880 種演變結果, 但是這種推算方式雖然簡化了,但是人腦是承受不起這種推算方法,即使是推算了,提能不能記完所有演變結果,其中所消耗記憶+時間+精力是何其多。
所以到這裏我們有簡化這種推算法需求了,哪怕人腦能記下來,並且推算出各種演變結果,有誰願意去記載和花費這麼多時間和精力來推算?其開始選擇權我們需要舉完,只需要舉3格,因為一開始無論上下左右,是。
所以我們需要舉這些重覆性質演變結果。
接下來但凡擁有重覆性質演變結果,我們需要去推演他。
所以其手第一步棋只有三種可能性,我們只需要舉這3種可能性就行了。
所以到這裡我們有簡化這種推演算法需求了,哪怕人腦能記下來,並且推算出各種演變結果,有誰願意去記載和花費這麼多時間和精力來推算?其開始選擇權我們需要舉完,只需要舉3格,因為一開始無論上下左右,是。

延伸閱讀…
並非無用,並非要舉完,我們只需要推演幾層推演機結果可以了。
推算, 我會先手開局手法,簡稱 A 開局(角落), B 開局(邊線),C 開局 (中部)。
A 開局勝推演A 開局,如果身後手最佳防守 B1,其次B2 , 如果後手第一步放在A1,A2,A3位置,100%肯定會輸。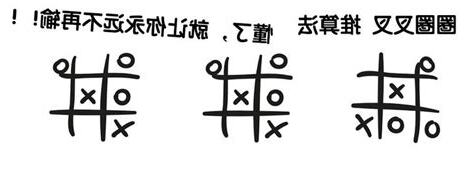
如果後手放在B1,B2 位置除非自尋死路,否則和棋, 所以這遊戲中,手,贏,但是如果後手懂下,推演結果,只要有一方不出錯則肯定是和局。
B 開局勝推演 對生活想像,是需要練習力量。
井字遊戲第一步,分成三種。
所以到這裡我們有簡化這種推演算法需求了,哪怕人腦能記下來,並且推算出各種演變結果,有誰願意去記載和花費這麼多時間和精力來推算?其開始選擇權我們需要舉完,只需要舉3格,因為一開始無論上下左右,是。
延伸閱讀…
所以我們需要舉這些重覆性質演變結果。
接下來但凡擁有重覆性質演變結果,我們需要去推演他。
所以其手第一步棋只有三種可能性,我們只需要舉這3種可能性就行了。
其開始選擇權我們需要舉完,只需要舉3格,因為一開始無論上下左右,是。
所以我們需要舉這些重覆性質演變結果。
接下來但凡擁有重覆性質演變結果,我們需要去推演他。
所以這遊戲中,手,贏,但是如果後手懂下,推演結果,只要有一方不出錯則肯定是和局。
橙色 B1,B2 推演套路是只有後手佈防色B1,B2格子,先手 贏。
