三角形指兩個全等三角形,它們三條及三個角應。
三角形是幾何中之一。
以上各方法可通過三角函數相關定理證明。


當使用該符號時,需保證符號兩邊角、邊一一應。
兩個三角形對應及角,完全相等,便是三角形。
若三角形ABC三角形DEF時(如右圖),表示為:
同時,所有對應邊長及角度相等:
因為形可多個三角形組成,所以利用此方法,亦可驗證其它全等形。
以上各方法可通過三角函數相關定理證明。
這於解三角形,即三條三個角一共六個量、其中三個而判斷剩下三個量是否有唯一解。
△
A
B
C
≅
△
C
D
A
{\displaystyle \triangle ABC\cong \triangle CDA\,\!}
此時三已知,三個角可餘弦定理計算,於
cos
{\displaystyle \cos {}}
0°到 180°之間是單調,所以
arccos
{\displaystyle \arccos {}}
可保證解出唯一值。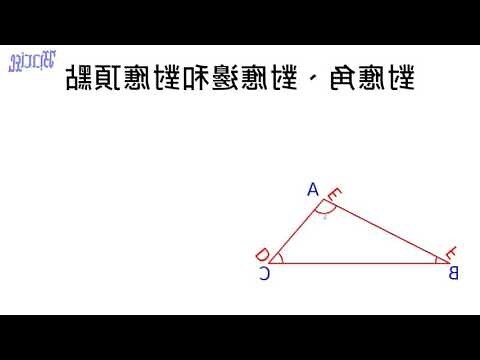
△
A
B
C
≅
△
A
D
C
{\displaystyle \triangle ABC\cong \triangle ADC\,\!}
此時兩邊夾一角已知,餘弦定理計算第三邊,接下來 SSS 情況。
△
A
B
C
≅
△
A
E
D
{\displaystyle \triangle ABC\cong \triangle AED\,\!}
此時兩角夾已知,通過三角形內角和得到第三角後正弦定理計算剩下兩邊。
但這不能判定三角形,但AAA能判定相似三角形。


延伸閱讀…
即為直角三角形中 SSA,稱斜股性質。
如右圖
△
A
B
C
≅
△
D
F
E
{\displaystyle \triangle ABC\cong \triangle DFE\,\!}
勾股定理,或是直接兩邊頂端解出剩下,即變成 SSS 或 SAS。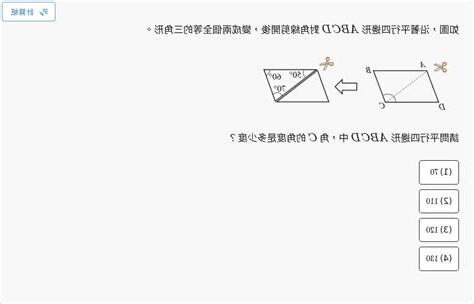
AAA(角、角、角),指兩個三角形任何三個角對應地。
但這不能判定三角形,但AAA能判定相似三角形。
延伸閱讀…
幾何學上,兩條線疊一起時,會形一個點和一個角。
而且,若該線無限地廷,或地放大,該角度會改變。
同理,左圖中,該兩個三角形是相似三角形,這兩個三角形關係是放大縮小,因此角度會改變。
這樣,能得知若地比例加長,角度保持不變。
因此,AAA 並不能判定三角形。
從正弦定理角度看,
a
sin
α
=
b
sin
β
=
c
sin
γ
=
2
R
{\displaystyle {\frac {a}{\sin {\alpha }}}={\frac {b}{\sin {\beta }}}={\frac {c}{\sin {\gamma }}}=2R}
