| 項 | 説明 |
|---|---|
| \( \nabla^2 u \) | 空間の二階微分 |
| \( \frac{1}{v^2} \frac{\partial^2 u}{\partial t^2} \) | 時間の二階微分 |
波の解とダランベールの式
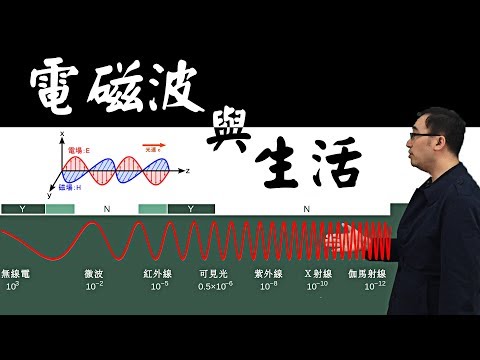
前節では、1次元の波の解法が紹介されていますが、本節では3次元の波の解について説明します。3次元の波 \( u(x, y, z, t) \) の波動方程式は、次式で表されます:


| 項 | 説明 |
|---|---|
| \( \nabla^2 u \) | 空間の二階微分 |
| \( \frac{1}{v^2} \frac{\partial^2 u}{\partial t^2} \) | 時間の二階微分 |
波の解とダランベールの式
前節では、1次元の波の解法が紹介されていますが、本節では3次元の波の解について説明します。3次元の波 \( u(x, y, z, t) \) の波動方程式は、次式で表されます:
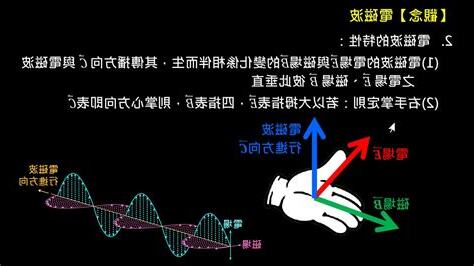
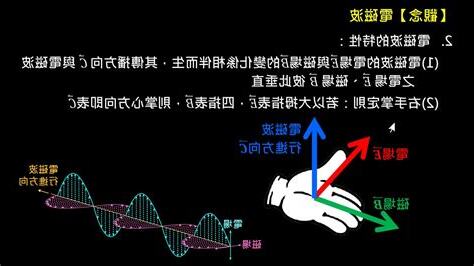
式 \eqref{eq:wave-eq-3dim} の最初の3つの項が空間上の各點での二階微分、左辺の最後の項が時間上の二階微分です。式 \eqref{eq:wave-eq-1dim} では、\( x \) の二階微分のみが扱われていましたが、3次元の波の場合は、\( x \)、\( y \)、\( z \) それぞれの二階微分の和をとる必要があります。

延伸閲讀…

式 \eqref{eq:wave-eq-3dim} の最初の3つの項が空間上の各點での二階微分、左辺の最後の項が時間上の二階微分です。式 \eqref{eq:wave-eq-1dim} では、\( x \) の二階微分のみが扱われていましたが、3次元の波の場合は、\( x \)、\( y \)、\( z \) それぞれの二階微分の和をとる必要があります。
延伸閲讀…
波動方程式の一般解は、\( f(t – x/v) \) と \( g(t + x/v) \) の和
波動方程式の簡略化
| 空間の各點で波の大きさと向きが定まるとき | \(\nabla^2 \bm{u} = 0\) |
ベクトル波の定義
- \(\bm{u}(x,y,z,t) = [u_x, u_y, u_z]\)
- \(\nabla^2 \bm{u} = \{\nabla^2 u_x, \nabla^2 u_y, \nabla^2 u_z\}\)
電磁場の記述
| 電場 | \(\bm{E}\) |
| 磁束密度 | \(\bm{B}\) |
電磁特徴量の関係
- \(\bm{D} = \varepsilon \bm{E}\)
- \(\bm{B} = \mu \bm{H}\)
- \(\varepsilon = \varepsilon_0 \varepsilon_r\)
- \(\mu = \mu_0 \mu_r\)
- \(n = \sqrt{\varepsilon_r \mu_r}\)
電場と磁場の波動方程式
電場の波動方程式
|
磁場の波動方程式
|
