八邊形是一種幾何形狀,擁有八條邊和八個頂點。八邊形的特點之一是它的內角和總是等於1080度。這種特性使得八邊形在幾何學中非常重要。
無論是正八邊形,凸八邊形,還是非凸八邊形,它們的內角和都遵循相同的規則。這是因為八邊形可以被切割成六個三角形,而每個三角形的內角和都是180度。因此,八邊形的內角和就是六個三角形的內角和,也就是1080度。


瞭解八邊形內角和的特性對於解決各種幾何問題非常有幫助。它是計算八邊形邊角和或證明兩個八邊形是否相似的關鍵。藉由充分理解八邊形內角和,我們可以更深入地探索幾何學的奧秘。
八邊形的幾何特性
在幾何學當中,八邊形,又稱為八角形,是指擁有八條邊和八個頂點的多邊形。它的內角總和為1080度,這個特性適用於所有的八邊形,無論是凸八邊形還是非凸八邊形。在這一節中,我們將探討八邊形的幾何性質,特別是正八邊形——一種所有邊等長、所有角等角的多邊形。
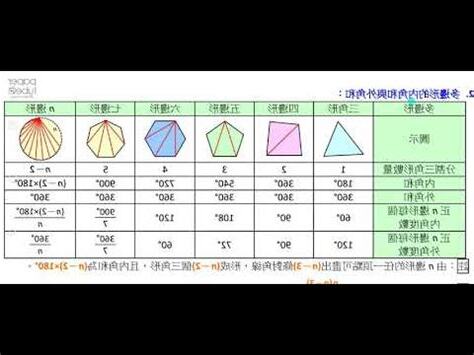
八邊形的內角和
由於任意多邊形的外角總和為360度,因此八邊形的內角和可以通過將外角總和乘以2來計算得出:
| 邊數 | 內角和(度) |
| 8 | 1080 |
正八邊形
正八邊形是一種特殊的八邊形,其邊長、角度皆相等。在施萊夫利符號中,它被表示為 {8}。由於正八邊形可以視為截去所有頂點的正方形,因此在施萊夫利符號中也可以表示為 t{4}。將正八邊形分割成兩個梯形和一個矩形,稱為八邊形-四邊形圖。
正八邊形的面積計算
給定正八邊形的邊長為a,其面積可以通過以下公式計算:
| 公式 | 面積(單位為原邊長的平方) |
| S = 8 * a | 當八邊形為矩形時,即兩組對邊分別平行且相等。 |
| S = 8 * (a / √2) | 當八邊形為正方形時,即所有邊都相等且對角線也相等。 |
這些公式基於八邊形的寬度S,該寬度等於次短對角線的長度。通過將八邊形分割成梯形和矩形,並應用三角函數,可以證明這些面積公式的正確性。
八邊形是一種有八個邊的多邊形。在幾何學中,研究八邊形的性質和特點是一個有趣的議題。其中一個重要的性質是八邊形內角和。
要計算任何多邊形內角和,我們可以使用以下公式:
內角和 = (n – 2) × 180°
其中,n代表多邊形的邊數。對於八邊形來説,n = 8,所以我們可以計算八邊形內角和:
內角和 = (8 – 2) × 180° = 1080°
這意味著八邊形的內角和等於1080度。
八邊形的內角分佈均勻,在八個內角中,每個內角都是相等的。這意味著每個內角的度數都是1080°/8 = 135°。
這個性質可以應用在很多實際問題中。例如,當我們知道兩個內角的度數,我們可以輕易計算出其餘內角的度數。
八邊形的特點
除了內角和這個重要的性質外,八邊形還有其他一些有趣的特點:
- 八邊形有8條邊和8個頂點。
- 八邊形的對角線有12條,其中任意兩條對角線不會重合。
- 八邊形可以分為兩個四邊形,每個四邊形的內角和等於360°。
- 八邊形可以透過對稱軸分為兩個對稱的四邊形。
這些特點使八邊形在幾何學中成為一個重要的形狀,也使得它在設計、建築和藝術等領域中被廣泛應用。
