對於債券收益的微小變化,久期可以給出利率敏感性測度。但隨着收益變化程度的增加,這種方法會產生越來越大的誤差。
這是因為債券價格隨利率的變化關係是非線性的。所以,我們需要再介紹一個概念,那就是債券的凸度。
債券凸度,也被稱為債券凸性,是債券價格(P)與到期收益率(y)之間的曲線關係。該曲線是凸向原點的,用來衡量債券價格收益率曲線的曲度。


説白了,就是債券每變動一個單位的收益率,對價格的影響不是按照一定比例變化的(即所謂的線性變化),而是非線性的,凸性就是衡量這種變化量的變化。
我們再通過一個簡單的例子説明下。
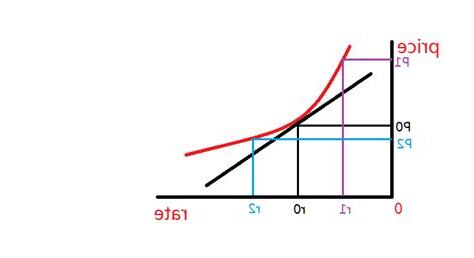
假設一隻債券收益率下降1%時,債券價格上漲1元,但當它的收益率下降2%時,價格可能上漲了2。
債券久期與凸度的重新理解
在債券投資中,久期和凸度是兩個重要的概念,它們用來衡量債券價格對利率變化的敏感性。久期可以被視為債券到期前的加權平均時間,而凸度則是用來描述債券價格隨到期收益率變化曲線的曲度。以下就這兩個概念提供一個不涉及複雜數學公式的解釋:
債券久期
債券久期可以用來衡量債券價格對利率變動的敏感程度。當利率上升時,債券價格會下降,而久期則告訴我們債券價格預計會下降多少。久期的計算依賴於債券的現金流特徵,比如每期支付的利息和最終的本金支付。債券的久期越長,意味著債券對利率變化的敏感性越高,即利率的小幅變化會導致債券價格的大幅波動。
債券凸度
債券凸度則是對債券價格與到期收益率之間非線性關係的一種度量。它考慮了利率變化對債券價格的影響不是簡單的一對一關係。債券的凸度越大,意味着債券價格對利率變化的反應越不穩定,即利率的小幅變化會導致債券價格的顯著波動。凸度可以幫助投資者理解利率變動時債券價格變動的不對稱性。
債券價格與利率的關係
債券價格與利率之間存在反向互動關係。當利率下降時,債券價格通常會上升,反之亦然。這種關係是非線性的,即利率的微小變化會導致債券價格的相對較小變化,而利率的顯著變化則會導致債券價格的顯著變化。債券凸度正是用來捕捉這種非線性關係的。
如何解釋凸度
想象一根彈簧,當你施加較小的力時,彈簧的伸長量較小;而當你施加較大的力時,彈簧的伸長量會急劇增加。債券價格對利率變化的反應類似於彈簧的行為:利率的小幅變化會引起債券價格的相對較小變化,而利率的顯著變化則會導致債券價格的顯著變化。凸度就是用來量化這種類似彈簧效應的指標。
總之,久期和凸度是債券投資中用以衡量利率風險的重要工具。投資者可以使用這些指標來評估債券組合對利率變動的敏感性,並進行相應的風險管理。雖然這些概念可能很複雜,但通過上述非數學化的解釋,我們可以對它們有一個更直觀的瞭解。
凸度是一個在幾何學和數學建模中常見的詞彙。它用於描述曲線或物體外形的特徵,並幫助我們瞭解其彎曲程度。對於設計師、建築師和工程師來説,瞭解凸度是十分重要的,因為它直接關係到設計和製造的品質。
凸度的概念可以追溯到古希臘時期,當時數學家亞裏士多德就對於圓和直線的關係進行了研究。他的理論奠定了現代幾何學的基礎,也為後來對凸度的定義和計算提供了依據。
在現代計算機科學中,凸度在許多領域都有應用,例如圖形處理、電腦動畫和模擬。通過精確計算和模擬物體表面的凸度,我們可以獲得更逼真的圖像效果和模擬結果。
凸度的計算方法
凸度的計算方法有多種,最簡單的方法是使用微分幾何學中的曲率計算公式。這個公式基於對曲線上兩個點之間的切線進行分析,並計算曲線在這兩點處的彎曲程度。
另一種常見的凸度計算方法是使用離散點和曲率向量。這種方法通常在計算機圖形學中使用,它將曲線或物體表面切分為許多小區域,並計算每個區域的凸度向量。通過這種方式,我們可以獲取更精確的凸度信息以及整個曲線或物體的外形特徵。
凸度不僅僅在數學和計算機科學中有應用,它還廣泛應用於許多不同領域。在工程設計中,凸度可以幫助我們確定物體的強度和穩定性。在建築設計中,凸度可以幫助我們設計出更美觀和符合人體工程學的建築結構。
此外,凸度在製造業中也有重要的應用。通過控制材料的凸度,我們可以製造出更精確和符合要求的產品。例如,在汽車和航空領域,精確的凸度控制可以確保零件之間的密合度和運動效能。
