「取捨原理是一個在組合數學中重要且有用的原理。在有限集合中,取捨原理可以幫助我們計算並理解不同子集的集合。這個原理可以通過容斥原理來表達,根據容斥原理,若有限集合A1,…,An,則整個集合的大小可以通過計算各個子集的大小,並且加減重疊部分得出。這個原理的應用廣泛,尤其在組合問題和計算問題中具有重要意義。」
\[\left|\bigcup_{i=1}^{n}A_{i}\right| = \sum_{i=1}^{n}|A_{i}| – \sum_{1\leq i
上式中,\(|A|\)表示集合\(A\)的基數。以兩個集合計算為例,我們可以先計算每個集合的大小,再減去它們交集的大小,即:
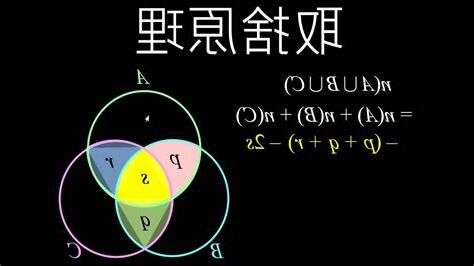
\[|A \cup B| = |A| + |B| – |A \cap B|.\]
排容原理可以用來依次計算多個集合併集的大小,通過對集合相交部分的大小進行加減抵消來達到目的。
| 集合 | 大小 | 相交部分大小 |
| \(A\) | \(|\!A|\) | – |
| \(B\) | \(|\!B|\) | – |
| \(A \cap B\) | \(|A \cap B|\) | – |
| \(A \cup B\) | \(|A \cup B|\) | \(|\!A|\) + \(|\!B|\) – \(|A \cap B|\) |
以此類推,對於更多的集合,我們繼續計算相交部分的大小並進行加減。這種方法可以避免重複計算相交部分的大小。
排容原理在解決多集合交集和併集的計算問題時非常有用,特別是在數據分析、圖論等領域。它是一個基於集合基本操作的重要原理。
「取捨原理」是一個在生活中非常重要的概念。它意味著我們在做出決策時,不得不優先考慮到一些重要的因素,同時也需要放棄一些不那麼重要的事物。這種原則適用於各個領域,包括工作、學習和人際關係等等。
在工作上,取捨原理可以幫助我們更好地管理時間和資源。當我們面臨多個任務時,我們需要依據其重要程度和時間限制,做出優先級的選擇。這麼做可以確保我們能夠專注於最關鍵的任務上,同時減少分散注意力和浪費時間的情況。
同樣地,在學習上也需要運用取捨原理。學習資源繁多,而時間有限。我們必須學會區分主次,選擇對我們個人發展最有價值的內容。這樣做能夠確保我們在有限的時間內獲得最大的知識收穫。
而在人際關係中,取捨原理同樣發揮著重要的作用。我們需要選擇我們的朋友圈子,關心和投入那些對我們最重要的人和事。同樣地,我們也需要避免那些對我們生活造成負面影響的人和環境。這樣做能夠讓我們有更多的時間和精力去經營那些真正關心我們的人和事。
