在幾何學中,八邊形,又稱八角形,是一種擁有八條邊和八個頂點的多邊形。八邊形的內角和為1080度。
八邊形有多種形式,其中最對稱的是正八邊形。其他八邊形根據其類角的性質可分為凸八邊形和非凸八邊形。

凸八邊形的內角角度皆小於180度,而非凸八邊形則可進一步分為凹八邊形和星形八邊形。星形八邊形是邊自我相交的八邊形。
所有八邊形都可以利用頂點切割成六個三角形,每個三角形的內角和為180度,因此所有八邊形的內角和都是1080度。

此外,任何多邊形的外角和都等於360度,因為它們最終會連回起點。
八邊形的幾何性質
| 性質 | 描述 |
|---|---|
| 內角和 | 所有八邊形的內角和為1080度。 |
| 凸八邊形 | 所有內角角度皆小於180度的八邊形。 |
| 非凸八邊形 | 包含凹八邊形和星形八邊形,後者具有邊自我相交的特性。 |
| 邊中心四邊形 | 在任何八邊形上構造的邊長與原邊長相同,且位於八邊形內部的正方形,其對角線會垂直且等長。 |
| 中點八邊形 | 將八邊形每個邊中點與相鄰邊中點連線成的八邊形,稱為對偶八邊形,其上有構造的正方形,其重心連心線的中點所構成的四邊形是正方形。 |
| 正八邊形 | 所有邊等長、所有角等角的八邊形,是正多邊形的一種。 |
| 面積公式 | 正八邊形面積可以用邊長a、外接圓半徑R或內切圓半徑r來計算。 |
| 分割性質 | 正八邊形可以被分割成兩個梯形與一個矩形,這種圖稱為八邊形-四邊形圖。 |
正八邊形作為截角正方形
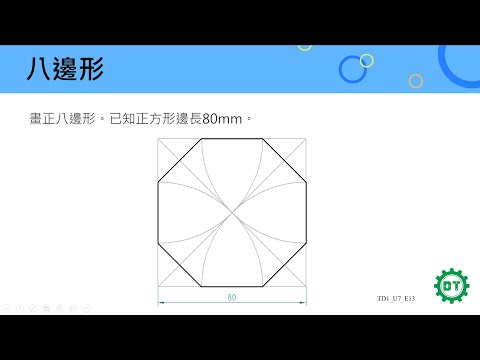
正八邊形可以視為截去所有頂點的正方形,即截角的正方形,因此在施萊夫利符號中也可以計為 t{4}。
另一方面,截角的八邊形為十六邊形,在施萊夫利符號計為 t{8}。正八邊形可以被分割成兩個梯形跟一個矩形,這種圖稱為八邊形-四邊形圖。
“`
八角形的美感與應用
八角形是一種具有獨特美感的幾何形狀。它擁有八個邊和八個角,給人一種堅固而有力的印象。它的對稱性和複雜性使它在設計和藝術領域中廣泛應用。
八角形在建築設計中常被用作裝飾元素。例如,古代中國的建築常常將八角形磚塊用於宮殿和寺廟的屋頂。這種設計給了建築獨特的視覺效果,同時也象徵著宮廷和宗教的神聖。同樣地,現代建築中也可以看到八角形的應用,它結合了傳統和現代的美學,創造出獨一無二的建築風格。
在藝術領域中,八角形被用來創作各種藝術品。畫家可以使用八角形作為畫面的基礎結構,將其他元素放置在八角形的各個角落,創造出獨特的藝術效果。此外,八角形還可以成為雕塑作品的形狀,藝術家通過雕塑的細膩觸感和對光線的巧妙運用,展現出八角形的美感。
八角形在幾何學中的特性
八角形在幾何學中有一些獨特的特性。首先,八角形是一種正多邊形,即它的八個邊長相等,八個內角也相等。這種對稱性使得八角形在幾何計算中非常方便。其次,八角形與圓形之間有一個特殊的關係,稱為「圓周角相等定理」。根據這個定理,八角形的內角和為360度,即八個內角的和等於一個圓的圓周角。
八角形還有一些有趣的性質。例如,如果將八角形的對腰線和對角線連接起來,就可以得到一個正方形。這個正方形的邊長是八角形的對腰線長的平方根。此外,八角形的對邊平行且相等,並且與八角形的對腰線垂直。這種特性使得八角形在幾何計算和設計中有廣泛的應用價值。
結論
八角形是一種具有獨特美感和豐富應用價值的幾何形狀。它在建築設計和藝術領域中被廣泛使用,為作品帶來獨特的視覺效果和美學體驗。在幾何學中,八角形具有一些特殊的性質,這些性質使得八角形在數學計算和設計中有重要的應用價值。無論是在設計還是在學術研究中,八角形都是一個充滿潛力和魅力的形狀。
延伸閲讀…
八邊形- 維基百科,自由的百科全書
406876 八角形圖片、庫存照片、3D 物體和矢量圖
