圓外角是數學中非常重要的概念之一。
圓外角存在於各種圖形中,並且在幾何學中起著關鍵作用。
它們在多邊形和特別是三角形中特別常見。


圓外角不僅指明圓形的特性,也能提供有關正多邊形和四邊形的有用信息。
這使得我們能夠更好地理解和分析這些形狀的性質。
一個多邊形的外接圓
圖形的構成與命名
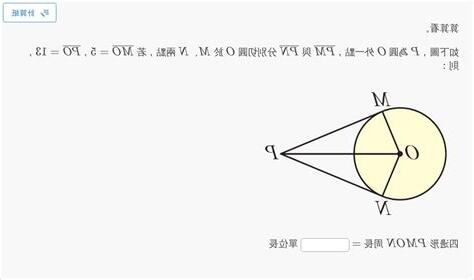
在數學中,當一個多邊形的所有頂點都位於同一個圓形上時,我們稱這個多邊形為圓內接多邊形,而這個圓被稱為多邊形的外接圓。如圖一所示,多邊形的頂點A、B、C、D分別與圓週上的點P、Q、R、S對應。圖中標示的∠APB、∠CPD、∠QPS都是圓外角。在圖二中,∠QPS是一個圓外角。
外接圓的應用
任何三角形都有一個外接圓,其外心的位置在三角形的三條邊的垂直平分線的交點上,並且到三個頂點的距離均相等。根據正弦定理,三角形的三邊與其對應角的正弦值成比例,即:
a / sinA = b / sinB = c / sinC = 2R
這裡,a、b、c分別表示三角形的三邊,R表示外接圓的半徑。由此可以推導出外接圓半徑的表達式:
R = (abc) / (4S)
其中,S是三角形面積,根據面積公式可以表示為S = (1/2)ab\sin C。
結語
總之,多邊形的外接圓是一個對數學研究非常有用的概念,對理解圖形幾何和空間關係具有重要意義。特別是三角形的所有外接圓都通過其外心,這一點在尺規作圖中非常有用。
圓外
圓外
一直以來,人們對於「圓外」這個詞彙總是抱有一種特殊的興趣。或許是因為這兩個字組合在一起時,所展現出的意象和含義總是讓人忍不住多想,也讓人不由自主地產生一股好奇心。圓外,似乎是一個神秘而未知的領域,藴含著無窮的可能。
「圓外」這個詞彙,從字面上看,就是指圓形的外部。然而,在這個世界上,我們往往會在範疇之外尋找一些超越常規的東西,對於某些人來説,「圓外」代表的是冒險和探索,尋找與眾不同的體驗。
許多故事和傳説中都存在著圓外的元素,不少人對於那些探索圓外的人物充滿敬佩。他們勇敢地面對未知,踏足未曾踏足的領域,發現那些隱藏在圓形界限之外的寶藏。
圓外也常常被譬喻為人類的夢想和渴望。夢想往往在生活的圓心裡誕生,然而,只有那些勇於跨越圓形邊界的人,才能讓夢想在圓外實現。他們從圓心出發,向著未知的方向勇敢前進,追尋屬於自己的圓外世界。
圓外不僅僅存在於物理的領域,也存在於心靈的世界。有時候,我們會在自己的思維和觀念之外找到解決問題的答案。這就像是一個迷宮,我們需要跳脱傳統的思維模式,以不同的視角去看待問題,才能發現圓外的解決之道。
總而言之,「圓外」是一個令人著迷且充滿可能性的詞彙。它代表了冒險、探索、夢想和思維的突破。我們應該勇於追尋自己的圓外世界,開拓屬於自己的新領域。
