梯形內角和是梯形的重要性質之一,它指的是梯形的底角和頂角的和。梯形是一種具有平行底邊和非平行腰的凸四邊形。根據梯形的定義,兩個底角和兩個頂角加起來得到的值稱為梯形內角和。
梯形的定義與性質
梯形(美式英語:trapezoid,英式英語:trapezium)是一種特殊的四邊形,其特徵是只有一組對邊平行。這兩條平行的邊稱為梯形的底邊,分別為上底和下底,而兩腰則是指梯形不平行的兩條邊。梯形的高是指下底與腰之間的距離,而底角是指下底與腰的夾角,頂角是指上底與腰的夾角。
梯形的幾何特徵
梯形的定義
梯形(英語:trapezoid)是一種特殊的四邊形,其特徵是只有一組對邊平行。這組平行的邊稱為梯形的底邊,而其他兩個邊則稱為腰。梯形可以進一步分為兩種類型:當上底不等於下底時,稱為不等的梯形;當上底等於下底時,則稱為等腰梯形。


梯形的高和中位線
梯形的高是指梯形的上底和下底之間的垂直距離。梯形的中位線是指連接梯形兩腰中點的線段。根據梯形的中位線定理,梯形的中位線與上底和下底都平行,並且等於上底和下底之和的一半。
梯形的高的計算
給出梯形的上底和下底的長度 a 和 b,以及腰的長度 c 和 d,且 a ≠ b,梯形的高 h 可以通過下式計算:
| 梯形高 | 計算公式 |
| 高 h | h = a + b / 2 |
梯形面積的計算
梯形面積 S 的計算公式為:
| 梯形面積 | 計算公式 |
| 面積 S | S = h × (a + b) / 2 |
“`
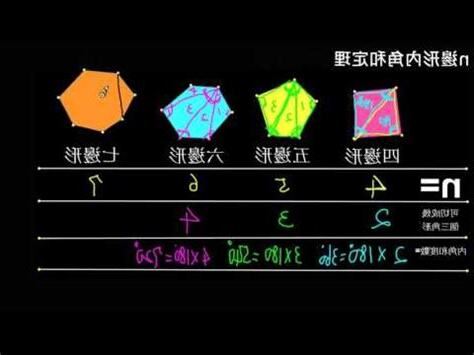
梯形內角和
梯形是一種特殊的四邊形,擁有兩組對立的平行邊。它有一些很有趣的特性,其中一個就是梯形內角和。
梯形內角和是指梯形內部的所有角度的總和。要計算梯形內角和,我們可以使用以下公式:
內角和 = 180° × (n - 2)
其中,n表示梯形的邊的數量。
讓我們來看一個例子:
<p><strong>例子</strong></p>
考慮一個梯形,具有兩組對立的平行邊和一對相鄰的角。假設梯形的兩對平行邊是AB和CD,相鄰的角是∠BCD和∠CDA。
根據梯形的性質,我們知道∠BCD和∠CDA的和是180°。所以,這個梯形的內角和是360°。
這只是一個簡單的例子,證明瞭梯形內角和的計算方法。對於複雜的梯形,使用相同的公式即可計算內角和。
