小輝將甲乙兩物體疊在一起的觀察讓我們得出了一個有趣的結論。
根據圖中顯示的情況,如果我們將甲乙視為一個物體,則有一半的體積在水面下。而由於水的密度為1,這意味著甲乙的平均密度為0.5。
換言之,我們可以得出結論:當物體的密度小於0.5時,在水面下的體積將小於整個物體的一半。


甲乙物體的沉浮分析
首先,我們有一個假設:甲乙可以看成一個整體物體,且這個整體物體有一半的體積在水面下。由於水的密度為1,我們可以得出甲乙的平均密度為0.5。既然甲的密度大於0.5,那麼乙的密度必然小於0.5。這排除了AB兩個選項。
進一步分析,當甲物體被移除後,剩下的乙物體密度小於0.5,因此它在水面下的體積必然小於原來整體物體體積的一半。根據浮力原理,物體密度越小,其在水中的浮力越大。因此,乙物體在甲物體被移除後,其浮力會增加。
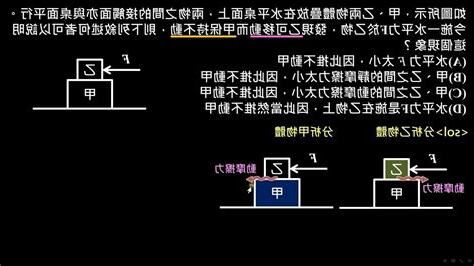
綜上所述,甲乙物體的沉浮特性符合圖示,因此答案選D。
浮力計算
當物體處於浮起狀態時,浮力等於物體的重力,即浮力等於物體密度乘以物體體積。因為浮力也等於物體在液麪下體積乘以液體密度,所以我們可以列式如下:
| 物體密度 | × | 物體體積 | = | 物體在液麪下體積 | × | 液體密度 |
這個等式是浮力原理的基礎,在此問題中應用於確定甲乙物體的浮力變化。
小輝將甲乙兩物體疊在一起
在這個故事中,小輝將甲乙兩個物體輕輕地疊放在一起。這個簡單的動作帶給他一種奇妙的感覺,彷彿時間停止了,世界靜止在這一刻。
小輝是一個喜歡探索和創造的人。他總是喜歡尋找新的方式來理解世界,並找到那些看似不可能的解答。所以有一天,他決定把甲和乙兩個物體放在一起,看看會發生什麼事情。
結果,當他輕輕地將甲放在乙上時,他驚訝地發現它們彼此完美地配合在一起。甲和乙的形狀和大小彼此呼應,就像是註定要在一起的一對。
小輝深深地被這美妙的景象所吸引,他想要更好地欣賞這個奇蹟,於是他找來了一把放大鏡。當他透過放大鏡觀察時,他看到了甲和乙之間微小而細緻的紋理,彷彿它們有著共同的秘密。
對小輝來説,這個疊放的動作不僅僅是將兩個物體放在一起那麼簡單。它代表著連接與共生的可能性,也代表著探索和發現的冒險。
小輝將甲乙兩物體疊在一起
小輝的職業是一位建築師,他利用他對疊放的概念的理解來創造出令人驚艷的建築作品。他相信物體之間的連接是建築的基礎,而疊放正是他創作的靈感之源。
他的作品被人們譽為是一種藝術,因為這些建築不僅僅是為了實用的目的,更是一種對連接和平衡的優美表達。
小輝的建築與眾不同,它們散發出一種獨特的美感,吸引著人們的目光。人們總是被那種疊放的形式所打動,彷彿看到了一個完美的和諧世界。
通過小輝將甲乙兩物體疊在一起的行為,我們可以看到人類的創造力和對連接的渴望。這樣的行為能夠激發我們心中的靈感,並帶給我們更多的美好。
