「最佳化理論」一詞在優化問題中扮演著重要角色。優化指根據一定標準,在一組方案中選擇最佳方案的過程,以最大化或最小化某一函數或變量。優化問題廣泛應用於計算機科學、工程學、運籌學、經濟學等領域中,數學界對其求解方法的發展一直予以關注。優化理論與技術在應用數學中佔據了重要地位,它能夠在給定定義域下,找到目標函數的最佳可達值。這樣的優化問題可根據變量的連續性或離散性分為兩類。」
連續優化與離散優化
- 連續優化: 變量是實數型,可以在一個連續的區間內取值。
- 離散優化: 變量是整數型或分類型,只能在有限的、離散的點上取值。
優化問題的表述
優化問題可以表述為在給定的定義域(或輸入)下,找到目標函數的「最佳可達值」。
目標函數與最優解
目標函數有多種稱呼,如判別函數、成本函數、效率函數等。最優解是指在滿足特定約束條件下,目標函數取最大值或最小值的點。
物理學與機器學習中的優化
在物理學中,通過能量最小化來找到系統的最優解。在機器學習中,模型質量通過損失函數來評估,找到損失函數極小值的點對應着一組可能的最優參數和最小的誤差。
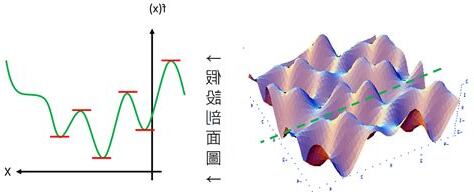
尋找極值點
極值點可能是局部的,意味着在該點附近的函數值不比該點的函數值大。極小值至少與附近的其他點一樣好,而最小值則至少與所有可行解一樣好。除非目標函數是凸函數,否則可能存在多個極小值。
凸優化與非凸優化的差別
在凸優化問題中,如果極小值位於可行集內且不是邊緣點,則它也是最小值。而在非凸優化問題中,可能存在多個極小值。
| 名詞 | 定義 |
|---|---|
| 最優化 | 選擇最佳方案的過程 |
| 連續優化 | 變量取值為連續的實數 |
| 離散優化 | 變量取值為整數或分類型 |
| 目標函數 | 用來衡量方案優劣的函數 |
| 極值 | 目標函數值達到最大或最小的點 |
| 極小值 | 在附近點中取最小值的點(局部最小值) |
| 最小值 | 在全部分可行解中取最小值的點(全局最小值) |
注意:以上內容僅供學習參考,不應用於商業用途或未經授權的出版。如果您有特定的優化問題需要解決,請諮詢相關領域的專家或使用專門的優化軟件。
最佳化理論的基本思想是通過搜尋最佳解決方案,使系統的性能達到最佳狀態。這可能涉及到優化目標函數,即需最大化或最小化的指標。例如,在生產過程中,我們可能希望最小化生產成本,或者最大化產品質量。最佳化理論可以幫助我們找到實現這些目標的最佳方法。
最佳化理論常常使用數學模型和算法來解決問題。它包括線性規劃、整數規劃、動態規劃等各種技術。通過將問題轉化為數學表達式,我們可以利用這些工具進行求解並找到最佳解決方案。
最佳化理論在現實世界中有許多應用。例如,在交通規劃中,最佳化方法可以幫助我們找到最有效的路線,從而減少交通擁堵。在物流管理中,最佳化理論可以幫助我們找到最佳的物流路線,節省成本並提高效率。
最佳化理論的應用不僅僅侷限於經濟領域。在科學研究中,最佳化方法可以幫助科學家找到最佳的實驗設計或最佳的參數配置,從而加速研究的進展。在機器學習和人工智能領域,最佳化理論經常用於優化算法的性能以及模型的設計和訓練過程。
