「方位角怎麼看」是一個常見的問題,方位角(azimuth angle)是從某觀察點的指北方向線起,到目標方向線之間的水平夾角。它是球座標系中的角測量,當應用到天體坐標時,方位角代表天空中恆星或天體在地平線上的方向。方位角的定義是從觀測者到感興趣點的向量投影正交到基準面,再計算投影向量與基準面上參考向量(指北)之間的角度。」
方位角的定義與應用
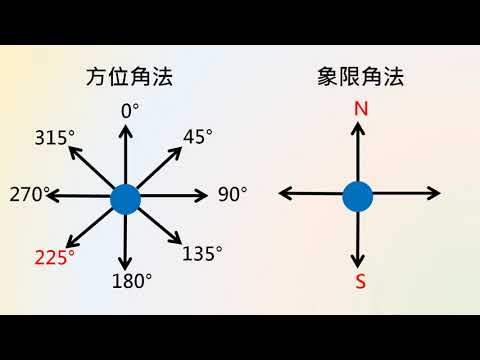
不同的定義與應用場合
方位角又稱為方位向或地平經度,是在球座標系中用來表示觀察點到目標方向線之間的水平夾角。這個概念常應用於天體坐標的測定,以及陸地和海洋導航中。方位角的英文「azimuth」源自阿拉伯語中的「as-sumūt」,意為「方向」。

天體坐標中的方位角
在天體天文中,方位角是指恆星或天體在地平線上的方向,從觀測者所在的半徑約5公里海平面上的地球表面量測。恆星是觀測者感興趣的點,而真北向量則是參考方向。方位角是恆星向量在水平面上的投影與真北向量之間的角度。

方位角在不同導航系統中的應用
在陸地導航中,方位角通常以α表示,並定義為從北方基線或子午線為基準量測的水平角。它在導航系統中通常有一個預先設定的基準面,且0°的方向可以從北或南開始,量測角度可以是順時針或逆時針。例如,方位角可以描述「從南向東30°」,縮寫為「S30°E」。總是先説明參考方向是北或南,再描述轉向東或西。選擇方向時,它們之間的角度是正的,在0到90度之間。如果方位角正好在基點的某個方向上,例如正東,則會標示為「正東」。
從平面座標計算方位角的方法
當平面上的兩個點的座標已知時,可以應用以下公式來計算地圖方位角。請注意,這裏的X軸和Y軸的順序與數學上的極座標相反,因為方位角是相對於北方順時針量測的。
計算公式
| 量測點座標 | 目標點座標 | 方位角 |
| X1 | X2 | atan2(Y2-Y1, X2-X1) |
這個公式中,X1和Y1是量測點的座標,X2和Y2是目標點的座標。atan2函數返回的是從北方順時針量測的角度的弧度值。
結語
方位角是一個重要的地理和航海概念,它在不同的應用場閤中有不同的定義和量測方法。瞭解方位角的基礎知識對於天文學、導航和其他相關領域的研究和實踐都至關重要。
方位角是指從一個參考點出發,以逆時針方向測量物體或位置相對於參考點的角度。方位角的計算可以用於導航、地理定位以及天文觀測等許多領域。
方位角的計算方法有多種,以下是其中幾個常見的方法:
- 磁北方位角:指的是物體或位置相對於磁北極的角度。
- 真北方位角:指的是物體或位置相對於地球真北極的角度。
- 地平方位角:指的是物體或位置相對於觀測者所在位置的地平面的角度。
要計算方位角,您需要知道參考點、目標位置以及使用的計算方法。例如,若您想知道一個地點相對於您所站的位置的方位角,您可以使用地平方位角的計算方法。
方位角的測量單位通常以度(°),但也可以使用其他單位,例如弧度(rad)。
總結來説,方位角是一種用於測量物體或位置相對於參考點的角度的方法。不同的計算方法可以應用於不同的情境,並且可以用於導航、地理定位和天文觀測等領域。
方位角計算的應用
方位角的計算在現代科技中具有廣泛應用,以下是一些常見的應用例子:
