「拉幾何學搭三角學中,直角,又稱正角,是角度為90度個角。渠相對於四分之一個圓周(即四分之一個圓形),因為拿圓周對應個圓心角劃分為360度,所以直角等於90度,而兩個直角便等於一個平角(180°)。角度比直角小個稱為鋭角,比直角大而比平角小個稱為鈍角。[1]」
「當兩條線個夾角是直角,箇兩條線便是互相垂直,是幾何上個一個重要性質。而一個三角形個其中一個內角為90°時,便稱為直角三角形,是應用畢氏定理個先決條件。」
「如果直線AB為圓形個直徑,箇麼取圓上個任何一點C所形成個三角形,∠ACB必為90°,是圓個其中一個性質,名為(半圓上個圓周角)。」

「拉弗同個應用上,直角有多種表示:」
直角的幾何性質與應用
什麼是直角?
在幾何學和三角學中,直角,也被稱為正角,是指角度為90度的角。它相對於圓周的四分之一(即圓的四分之一),因為將圓周對應的圓心角分為360度,所以直角等於90度,而兩個直角等於一個平角(180°)。小於直角的角稱為鋭角,大於直角但小於平角的角稱為鈍角。
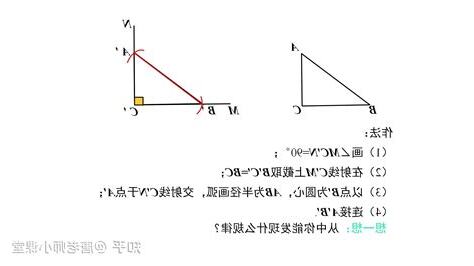
直角的特殊性質
當兩條線的夾角是直角時,這兩條線互相垂直,這是幾何中的一個重要性質。在一個三角形中,如果其中一個內角是90°,那麼這個三角形稱為直角三角形,它是應用畢氏定理的先決條件。
直角的圓周角性質
如果直線AB是圓的直徑,那麼在圓上任意取一點C,所形成的三角形∠ACB必為直角,這是圓的一個性質,稱為(半圓上的圓周角)。
直角的表示方法
在不同的應用中,直角有多種表示方式:
- 在三角形中,直角用表示為
∠ABC = 90°或∠ACB = 90°。 - 在直角三角形中,通常使用大寫的英文字母 “V” 或 “L” 來表示直角。
- 在建築或工程圖中,直角通常用 “
” 或 “ ” 來表示。
直角在幾何學和工程學中扮演着基礎性的角色,不僅在三角學中用於計算,也在平面的直線和曲線關係中提供了解決問題的基準。
直角的定義 |
直角是指角度為90度的角。 |
直角三角形 |
三角形中有一個內角為90°的三角形稱為直角三角形。 |
半圓上的圓周角 |
當直線AB是圓的直徑,在圓上任意取一點C,所形成的三角形∠ACB必為直角。 |
通過這些概念,我們可以理解直角在幾何學中的重要性和廣泛應用。
直角,作為幾何學中的基本概念之一,是指兩條相交的直線所形成的角度為90度的角。這個特殊的角度讓直角在許多數學和工程應用中具有重要地位。
直角三角形
直角三角形是一個至少有一個直角的三角形。根據勾股定理,直角三角形的兩個邊長的平方和等於斜邊長的平方。這個定理在許多實際問題中有廣泛的應用,例如測量地形的高度、計算房屋的角度以及設計橋樑和建築等。
直角坐標系統
直角坐標系統是描述二維平面中點位置的一種方法。它使用水平軸和垂直軸上的數字來標示每個點的位置,這樣的坐標系統也稱為笛卡爾坐標系統,以法國數學家笛卡爾的名字命名。
在直角坐標系統中,水平軸被稱為x軸,垂直軸被稱為y軸。每個點可以通過它們在x和y軸上的位置來表示,例如(x, y)。這種坐標系統在幾何學、物理學、計算機圖形學等領域中被廣泛應用。
直角投影
直角投影是一種將三維物體投影到二維平面上的方法。最常見的直角投影類型是正交投影,其中投影線垂直於投影平面。這種投影方法在建築、工程和圖形學中被廣泛使用,以便更容易地觀察和分析三維物體的形狀和結構。
直角編程
直角在程式設計中也扮演著重要的角色。使用「if」和「else」語句,我們可以根據特定條件執行不同的程式碼塊。這樣的程式碼分支結構可讓我們根據不同的情況進行相應的操作,實現更靈活和多樣化的程式邏輯。
結論
直角是幾何學中一個重要且有趣的概念,它在數學、工程和程式設計中都有廣泛的應用。希望透過這篇文章,您能對直角的意義和相關應用有更深入的瞭解。
直角坐標系統
直角坐標系統是描述二維平面中點位置的一種方法。它使用水平軸和垂直軸上的數字來標示每個點的位置,這樣的坐標系統也稱為笛卡爾坐標系統,以法國數學家笛卡爾的名字命名。
在直角坐標系統中,水平軸被稱為x軸,垂直軸被稱為y軸。每個點可以通過它們在x和y軸上的位置來表示,例如(x, y)。這種坐標系統在幾何學、物理學、計算機圖形學等領域中被廣泛應用。
直角編程
直角在程式設計中也扮演著重要的角色。使用「if」和「else」語句,我們可以根據特定條件執行不同的程式碼塊。這樣的程式碼分支結構可讓我們根據不同的情況進行相應的操作,實現更靈活和多樣化的程式邏輯。
延伸閲讀…
直角- 維基百科,自由的百科全書
直角三角形_百度百科
