「圓形分三等份」是一個有趣的幾何問題,只需將圓周分為三個相等的圓弧,即可將圓等分為三份。每個圓弧所對的圓心角都是120°,使得圓形被分成平均的部分。有多種方法可以實現這個目標,其中一種最簡潔的方法是以A為圓心,用AO作為半徑作圓,在⊙O上與C、D兩點相交。因為OA=OD=AD,所以∠DOA=60°。同樣地,∠AOC也是60°。因此,∠DOC等於120°。再以C為圓心,用CD作為半徑作圓,在⊙O上與點E相交。由於CE=CD,所以∠COE=120°,並且∠EOD也等於120°(360°的周角)。通過連接OC、OD和OE,可以看出這三段線段平分了⊙O。對於不知道圓心的情況,可以利用圓周角和圓心角之間的關係來解決問題。
利用圓規與直尺,可以巧妙地將圓分成相等的三部分。這裡介紹幾種不同的方法,這些方法基於幾何原理,並且不依賴於計算。首先,我們需要瞭解一個事實:圓周角等於該弧相對的圓心角的一半。這個事實將幫助我們在沒有直角尺的情況下將圓三等分。
-
已知圓心時的方法
當你知道圓心的位置時,可以採用以下簡潔的方法:
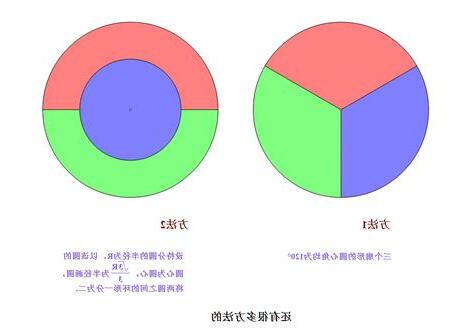
- 以圓心A為基準,用圓規畫出一個半徑為RA的圓,交原圓於點C和點D。因為OA=OD,所以∠DO A為60°。同理,∠AOC也是60°。因此,∠DOC為120°,這就是我們要求的圓心角。
- 再以點C為圓心,CD為半徑畫圓,交原圓於點E。因為CE=CD,所以∠COE為120°,進而∠EOD也是120°。
- 連接過O點的三條線段OC、OD、OE,這樣就將原圓分成了三等份。
-
未知圓心時的方法
如果不知道圓心的位置,可以使用以下方法:
- 以原圓上任意一點A為正三角形的頂點,利用圓規畫出正三角形剩下的兩點B和C。
- 以點E為圓心,ED為半徑畫弧,交原圓於點F。因為DE是正三角形的一邊,所以∠DOE為60°,進而∠EOD為120°。
- △FED為正三角形,連接其頂點與垂心(三心合一)的連線,這條線將原圓三等分。
| 方法 | 步驟 |
|---|---|
| 已知圓心 | 2, 3, 4 |
| 未知圓心 | 1, 2, 3, 4 |
總之,透過應用幾何原理,可以利用圓規和直尺將圓三等分,而不需要進行複雜的計算。這些方法可以幫助我們在實際生活中快速解決圓分類的問題。
圓形分三等份是一個有趣且具有挑戰性的幾何問題。這個問題可以通過幾種方法來解決,並且在許多不同的領域中都有應用。
首先,讓我們從一個簡單的方法開始。假設我們有一個完美的圓形,並且希望將其分成三等份。我們可以使用一個等邊三角形作為模板,將其放置在圓形中央,並且必須確保每個頂點都與圓形的周圍相切。
然而,這種方法有點困難,因為我們需要精確地將等邊三角形放置在圓形中,並且需要進行精確的測量。因此,還有其他方法可以解決這個問題。
一種常見的方法是使用一種稱為「分割圓弧」的技術。這種方法使用一個圓形的弧,並將其分成等份。然後,我們可以將這些等份連接起來,並形成圓形的三等份。這是一種相對簡單且易於理解的方法,並且可以在不同的場閤中應用。
應用
圓形分成三等份的問題在許多不同的領域中都有應用。在建築和設計中,這個問題可以用於創造對稱和平衡的結構。例如,建築師可以使用這個問題來設計創新的建築物,並且可以在不同的元素中應用這個概念。
此外,在數學和幾何學中,圓形分三等份的問題可以用於研究形狀和幾何關係。這個問題涉及到圓形的對稱性和角度的計算,並且可以幫助我們更好地理解幾何學的基本概念。
此外,在藝術和設計中,圓形分成三等份的問題可以用於創作藝術品和設計作品。藝術家可以使用這個問題來創造獨特而美麗的藝術品,並且可以將這個概念應用到他們的創作中。
圓形分成三等份是一個有趣且具有挑戰性的問題,在許多不同的領域中都有應用。無論是建築、數學、藝術還是設計,這個問題都可以幫助我們更好地理解形狀和幾何關係,並且可以應用到創新的領域中。
希望這篇文章對您有所幫助!如果您有任何其他問題,請隨時讓我知道。
延伸閲讀…
三等分圓面積
怎麼把圓形的蛋糕平均分成三等份
