[三點求圓]應當是在座標中討論的問題,因此,首先需要明確,圓的一般公式為:$x^2 + y^2 + Dx + Ey + F = 0$。三點設為 $(x_1, y_1)$、$(x_2, y_2)$、$(x_3, y_3)$,代入此公式後,即可得出半徑 $R = \sqrt{\frac{D^2 + E^2 – 4F}{2}}$,並得出圓心 $O(x_0, y_0)$ 的座標為 $(-\frac{D}{2}, -\frac{E}{2})$, 再將其帶回標準方程即可。
三點求圓中,圓心落在兩條中垂線的交點處,先用直線方程來計算兩點間距,再用中垂線的特色,即斜率相乘為 $-1$,及兩點求的中點公式,得出兩條中垂線的直線方程,將此兩條方程代入,即可得出圓心座標,再將此圓心與三點中隨便一點求間距,即得到 $R$,代入圓的標準式,即可算出其方程。
在座標系的架構之下,圓的問題,皆可藉由其半徑及圓心來解決;圓的標準式及一般式的已知項,僅有 $3$ 個變量需求解,因此三點求解即可求出其座標。通常會使用一般式進行代入計算,原因在於變量的指數都在一次方上;而標準式,在 $R = 0$ 時,僅有兩條變量,將成為最為簡便的 二元二次方程式 問題。只要分析出題目中的訊息,即可寫出相應之方程式組進行解決問題。


簡要説明一下,其主要的原理是:$a(x, y) – a(x_3, y_3)$ 與 $ b(x, y)$ 的乘績與 $r$ 的比率為 $a(x_3, y_3)$,而 $ b (x3, y3)$ 的乘績與 $a(x, y$ 的比率為 $-r$;因此,圓即為: $a(x,y) + b(x,y) = 0$,展開即為:$(x−x0)2+y−y0)2=r2$。
若利用 [高斯─若當消去法][5] 來解題,那麼當沒有交點的情況下,表示點是共線的,無法畫出圓。在最近撰寫的軟體之中,必須根據指定的座標點,繪出相應的圓形。因此,針對相關的演算公式進行推論,其推論的難度不高,主要作為備忘錄來使用。設圓的圓心座標為 $O(x_0, y_0)$, 其半徑為 $r$,圓的方程可寫成:$(x−x0)2+(y−y0)2=r2$;若圓上取點, 分別取為 $A(x_1,y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$。則可得:
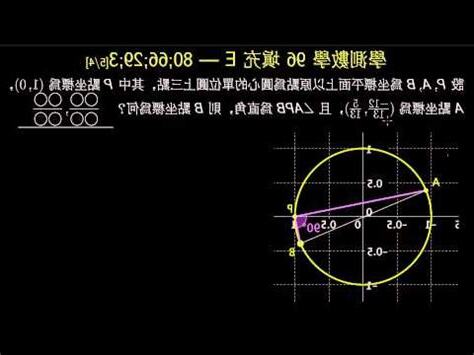
由公式 $(1) 、(2)$ 作差運算:
$$\begin{split} x_1x2-x_3x2-x_1^2+x_2^2+y_1y_2 -y_2y_3- y_1^2+y_3^2 &= 0, \\ 2(x_2-x_3)x_3 &= 0, \\ 2( y_1-y_3) y_3 &= 0. \end{split}$$
由公式 $(1)、、(4)$ 作差計算:
$$\begin{split} -2(x2-x3)x_2 + 2(y2-y3)=0 , \\ -x_3y3-y_1y3 -x_3x2- x_1x2 +x_1y_1 +y_2y_3 &=0. \end{split}$$
由上述運算可以得到:
$$\begin{align} x &= \frac{|\begin{bmatrix} x_3 & y_3 & 2x_3\\ x_3 & y_3 &2y_3 \\ x_3 & y_3 &2 \end{bmatrix} |}{|\begin{bmatrix} 2(x_2-x_3)& 0 \\ 0 &2(x_1 -x3) \\ -2(x_2-x_3)& 2(x_2-y_3) \\ \end{bmatrix} |} \\ y &= \frac{ |\begin{bmatrix} 2(x_2-y_3) & 0 \\0&2y_1-2y_3\\ -y_3-y_3 & y_3-y_3\end{bmatrix} |}{| \begin{bmatrix} 2(x_2- x_3) &0 \\ 0 &2 (x_1-x_3)\\ – 2(x_2 -x_3)& 2(x_2-y_2) \\ \end{bmatrix} | }\end{align} $$
其中,分母的行列式需要不等於0,也就是:
$$\begin{vmatrix} 2(x2-y_1) & 0 \\ 0 & 2 (x_1 -x_1) \\ -(x_3+y_3) & 2y_3-y_3 \\ \end{vmatrix} \neq 0$$
換句話説,當三點共線的時候,並不能形成圓,而半徑 $ r$ 可以由下列公式算出:
$$\begin{split} r &= \left| \frac{\begin{bmatrix} x_1^2+y_1^2 & x_1 & y_1 & 1\\ x_2^2 +y_2^2& x_2& y_2& 1 \\ x_3^2+y_3^2 &x_3 & y_3& 1\end{bmatrix}} {\begin{bmatrix} 0 & -2y_2 & 2y_1 \\ 2x_2 & -2x_2 & 2x_2 \\ 2(x_2- x_3) & -(x3+y_1) & 2y_3-y_3 \end{bmatrix}} \right| \\ &= \sqrt{\frac{-|\begin{bmatrix} x3 & y2 & 1 \\ x2 &y_3 & 1 \\ x_3 & y_2& 1 \end{bmatrix}|}{2(x_2 -x_3) }} \end{split}\tag{6}$$
由此可知,三點求圓,已獲得解答。
[高斯─若當消去法]: 高斯─若當消去法是一種用於求解線性方程組的數學方法,其原理為:在不改變方程組的解的情況下,對方程組進行以下操作:(1) 交換兩個方程式的位置;(2) 乘其中一個方程式一個非零的常數;(3) 將其中一個方程乘以一個非零常數,並加到另外一個方程式。
三點共線: 三點連成的線段位於同一條直線上。
三點成圓:探究圓的內在性質
「三點成圓」這一説法,揭示了圓形與三點之間的密切關係。在幾何學中,三點可以確定唯一的圓,而圓心位於三點形成的三角形內。
三點成圓的條件
三點成圓的條件十分簡單:
| 條件 | 説明 |
|---|---|
| 三角形內角和為 180 度 | 三點共線時,內角和為 180 度。 |
| 三角形內角和不為 180 度 | 三點不共線時,內角和不為 180 度。 |
三點確定圓心的方法
三點可以確定圓心,有以下兩種方法:
1. 中垂線法
- 繪製三點連線的中垂線。
- 中垂線交於一點,該點即為圓心。
2. 角平分線法
- 繪製三點連線的角平分線。
- 角平分線交於一點,該點即為圓心。
三點成圓的應用
三點成圓在幾何學和工程中具有廣泛的應用,例如:
延伸閲讀…
通過三個定點的圓的方程
三點確定一個圓的計算方法原創
- 圓作圖:利用三點可以構造一個圓。
- 圓定理:與圓相關的定理,如圓心角定理、圓周角定理,都基於三點成圓的性質。
- 圓錐曲線:圓錐曲線(圓、橢圓、拋物線、雙曲線)的性質與三點成圓有關。
- 機械設計:利用三點成圓可以設計傳動機構,如齒輪、軸承等。
結語
「三點成圓」這一性質揭示了圓形與三點之間的深層聯繫。通過三點可以確定唯一的圓,並進一步探索圓的豐富性質。這一原理在幾何學、工程和日常生活中都有重要的應用價值。
