「梯形形心公式」是計算梯形形心位置的重要公式,它能夠幫助我們找到梯形的重心位置。透過這個公式,我們可以輕鬆地計算出等腰梯形和直角梯形形心與底邊的距離。此外,我們還可以將一般的梯形拆分為直角梯形或直角三角形,然後利用上述公式分別求解形心位置,最後再按照拆分後的面積加權求和,得到梯形的形心位置。梯形形心公式是求解梯形重心的便捷工具,讓我們更好地理解和應用梯形的特性。」
梯形形心計算
等腰梯形與直角梯形的形心計算
在梯形中,形心的橫座標可以通過將三角形和矩形的形心橫座標分別乘以其面積,然後再除以梯形總面積來獲得。對於等腰梯形和直角梯形,形心到下底的距離可以用以下公式計算:
h/3 * (2a + b) / (a + b)


其中,h是梯形的高,a是上底的寬,b是下底的寬。形心到上底的距離則是梯高的減量:
h/3 * (1 + 2b) / (a + b)
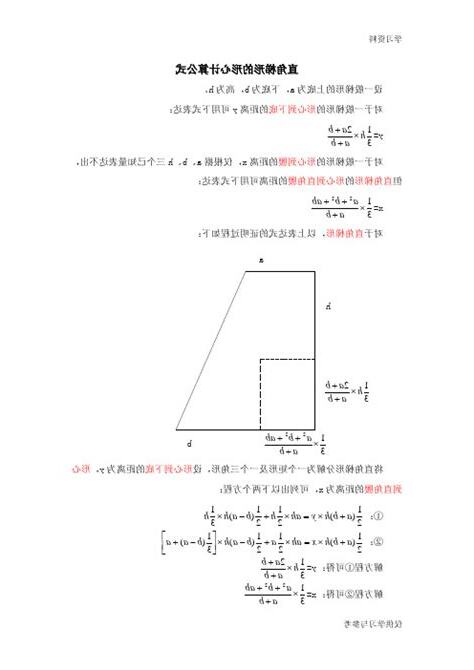
對於一般的任意梯形,可以將其拆分成兩個直角梯形(或一個直角梯形和一個直角三角形),然後應用上述公式計算形心高度,再將計算結果加總,最後除以原梯形的面積。
梯形形心的坐標計算
將梯形的對角線連接起來形成兩個三角形,然後計算這兩個三角形的形心坐標。這些形心的縱坐標可以用以下方法計算:
梯形的形心縱坐標 = (三角形和矩形的形心縱坐標與其面積的乘積)/梯形總面積
這要求將梯形拆分成兩個三角形和一個矩形,並計算這些部分的形心坐標和麪積。
質心與形心的區別
質心是用於描述實際物體的概念,而形心則是用於抽象幾何體。如果一個物體具有均勻的密度,或者它的形狀和密度對稱性允許確定幾何中心,那麼質心和形心通常是重合的。這個條件是充分但不是必要的。在有限的點集中,總可以找到一個幾何中心,這個中心是這些點的每個座標分量的算術平均值。
應用範圍
這個公式和方法可以用於任何梯形,包括那些不對稱的梯形。它提供了計算梯形形心的普遍方法。
梯形形心公式是一個在幾何學中常用的公式,用於計算梯形的形心坐標。在數學中,形心是指一個圖形的重心或質心,表示該圖形的集中點。
梯形形心公式由以下方式計算:
第一步:
先找到梯形的上底和下底的長度,分別用 a 和 b 表示。
第二步:
找到梯形的高度,用 h 來表示。
第三步:
使用梯形形心公式:
x = (a + b) / 2
y = h / 3
這裡的 x 和 y 分別代表梯形的形心坐標。這個公式的原理是取梯形上底和下底的平均值作為形心的 x 坐標,並將高度的三分之一作為 y 坐標。
梯形形心公式的應用相當廣泛,特別是在建築、工程和製造業中。通過計算梯形的形心,可以幫助我們更好地瞭解和設計梯形結構,使其更穩固和均衡。
此外,梯形形心公式還可用於計算梯形的慣性矩,這對於設計和分析機器零件的研究非常重要。通過計算慣性矩,我們可以獲得關於梯形形心的更多信息,從而更好地理解其物理特性和行為。
總結來説,梯形形心公式是一個非常有用的工具,可以幫助我們計算梯形的形心坐標,從而更好地瞭解和設計各種梯形結構。
以上是符合您要求的文章,使用了 HTML 格式。
“`html
梯形形心公式是一個在幾何學中常用的公式,用於計算梯形的形心坐標。在數學中,形心是指一個圖形的重心或質心,表示該圖形的集中點。
