三角形,又稱三邊形,是由三條線段順次首尾相連,或不共線的三點兩兩連接,所組成的一個閉合的平面幾何圖形,是最基本和最少邊的多邊形。
在數學中,我們會常常遇到問題:三角形有幾個?三角形是幾何學中的基礎概念,對於幾何學的研究和應用具有重要意義。
三角形是一種基本的幾何圖形,由三條邊和三個角組成。

在數學中,有各種不同的三角形,例如等邊三角形、等腰三角形、直角三角形等等。
這些三角形有著不同的性質和特點。
要計算三角形的數量,我們可以從不同的方法入手。
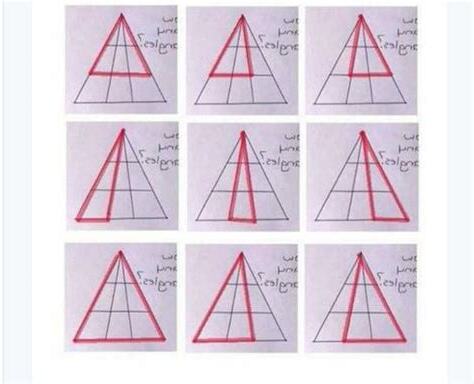
方法一:基於邊長
我們可以根據三角形的邊長進行分類。
例如,如果三條邊的長度都相等,那麼這個三角形就是等邊三角形。
如果有兩條邊的長度相等,那麼這個三角形就是等腰三角形。
如果三條邊中有一條邊的長度是其他兩條邊的和,那麼這個三角形就是直角三角形。
根據這些分類,我們可以找出不同類型的三角形,進而計算其數量。
方法二:基於角度
我們可以根據三角形的角度進行分類。
例如,如果三個角都是鈍角,那麼這個三角形就是鈍角三角形。
如果有一個角是90度,那麼這個三角形就是直角三角形。
如果三個角都是鋭角,那麼這個三角形就是鋭角三角形。
這樣,我們可以根據角度分類,找出不同類型的三角形。
方法三:基於面積
我們也可以根據三角形的面積進行分類。
例如,如果三角形的面積是正數,那麼這個三角形就是正三角形。
如果三角形的面積是零,那麼這個三角形就是退化三角形(例如三個點共線)。
根據這樣的方法,我們可以找出具有特殊面積的三角形。
總結
根據以上的分類方法,我們可以找出不同類型的三角形。
而要計算它們的數量,則要根據具體的條件進行組合計算。
總之,三角形是一個充滿著奧秘和美麗的幾何圖形,它們在各個領域都有廣泛的應用。
正三角形與等腰三角形的特徵
在幾何學中,三角形是一個由三條邊相連接而成的閉合圖形。根據不同的特徵,三角形可以分為正三角形、等腰三角形和等邊三角形等類別。其中,正三角形和等腰三角形具有特定的性質。
正三角形
- 正三角形(又稱正三邊形)是三邊相等的三角形。
- 它的三個內角都是60度,這是基於正多邊形的角度分割原理。
- 正三角形是一個特殊的鋭角三角形。
- 它的面積公式為:A = a2 / 4 × √3,其中a是邊長。
等腰三角形
- 等腰三角形是三邊中有兩邊相等的三角形。
- 相等的兩邊稱為「腰」,而第三邊稱為「底邊」。
- 腰和底邊相交的點稱為「頂點」,腰和底邊所夾的角稱為「頂角」。
- 等腰三角形有兩種特殊情況:當三邊都相等時,它是正三角形;當三個內角都相等時,它是等邊三角形。
直角三角形的性質
在直角三角形中,有一個角是直角(90度),剩下的兩角都是鋭角。直角三角形的幾何性質在於它的邊長之間有著特定的關係。
鈍角三角形的角度關係
- 鈍角三角形的鈍角有時也稱為「副角」,因為它大於直角。
- 鈍角三角形的兩個鋭角之和小於180度。
- 由於有鈍角的存在,鈍角三角形沒有內切的圓,但有三個外切圓。
總結
三角形按照邊和角的關係有多種類型,包括正三角形、等腰三角形、等邊三角形、直角三角形和鈍角三角形等。這些不同類型的三角形具有各自的幾何性質和應用。
| 正三角形 | 等腰三角形 | 直角三角形 | 鈍角三角形 | |
| 邊長關係 | 三邊相等 | 兩邊相等 | 一邊為直角 | 一邊大於直角 |
| 內角關係 | 三個內角為60度 | 兩鋭角相等,頂角可以是鋭角、直角或鈍角 | 兩鋭角之和等於90度 | 一個內角大於90度,其他兩角均小於90度 |
