勢阱(英語:Potential well)是一個包圍着勢能局部點鄰域。
勢阱捕獲能量轉化其它形式能量(例如能量從重力勢阱中逃脱轉化動能),因為它勢阱局部點捕獲。
因此,一個勢阱捕獲物體不能繼續全局勢能處運動,即使它熵原理地傾向於全局點運動。
截然不同地,量子力學裏,雖然粒子能量於阱壁位勢,阱外找到粒子機率於0。

勢阱捕獲能量轉化其它形式能量(例如能量從重力勢阱中逃脱轉化動能),因為它勢阱局部點捕獲。
因此,一個勢阱捕獲物體不能繼續全局勢能處運動,即使它熵原理地傾向於全局點運動。
量子力學裏,方形阱,稱為深位勢阱,是無限深方形阱延伸。
方形阱是一個阱內位勢0,阱外位勢值位勢阱。
關於一個或多個粒子,這種位勢作用中量子行為問題,稱為深位勢阱問題。
無限深方形阱問題是,阱外找到粒子機率於0。
經典力學裏,假若,粒子能量於阱壁位勢,則粒子只能移動於阱內,無法存在於阱外。
截然不同地,量子力學裏,雖然粒子能量於阱壁位勢,阱外找到粒子機率於0。
一維方形阱阱
L
{\displaystyle L\,\!}
,左邊阱壁右邊阱壁位置
x
=
−
L
/
2
{\displaystyle x=-L/2\,\!}
與
x
=
L
/
2
{\displaystyle x=L/2\,\!}
。
阱內位勢0。
阱壁,位勢突然升高為
V
0
{\displaystyle V_{0}\,\!}
。
阱外位勢保持為
V
0
{\displaystyle V_{0}\,\!}
。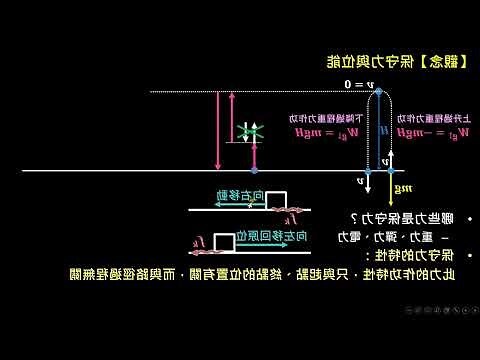
這一維阱整個一維空間分為三個區域:阱左邊,阱內,阱右邊。
每一個區域內,應著位勢,描述粒子量子行為波函數
ψ
{\displaystyle \psi \,\!}
,標記:[1]:78-82
這些波函數,滿足,一維不含時間薛丁格方程式:
其中,
ℏ
{\displaystyle \hbar \,\!}
是約化普朗克常數,
m
{\displaystyle m\,\!}
是粒子質量,
x
{\displaystyle x\,\!}
是粒子位置,
V
(
x
)
{\displaystyle V(x)\,\!}
是位勢,
E
{\displaystyle E\,\!}
是能量。
阱內,位勢
V
(
x
)
=
0
{\displaystyle V(x)=0\,\!}
,方程簡化:
設定波數
k
{\displaystyle k\,\!}
為
這是一個多研究二階常微分方程。
總結前面導引出結果,波函數
ψ
{\displaystyle \psi \,\!}
形式為:
當
x
{\displaystyle x\,\!}
趨向負無窮,包含
F
{\displaystyle F\,\!}
項目趨向。


延伸閱讀…
阱外,位勢
V
(
x
)
=
V
0
>
0
{\displaystyle V(x)=V_{0}>0\,\!}
,薛丁格方程為:
視能量是否於位勢而定,有兩種解答。
一種是粒子解答,另一種是束縛粒子解答。
假若,粒子能量於位勢:
E
<
V
0
{\displaystyle E
設定
解是指數函數。
所以,阱左邊區域阱右邊區域波函數是
其中,
F
{\displaystyle F\,\!}
,
G
{\displaystyle G\,\!}
,
H
{\displaystyle H\,\!}
,
I
{\displaystyle I\,\!}
是常數。
邊界條件,可以找到常數
A
{\displaystyle A\,\!}
,
B
{\displaystyle B\,\!}
,
F
{\displaystyle F\,\!}
,
G
{\displaystyle G\,\!}
,
H
{\displaystyle H\,\!}
,
I
{\displaystyle I\,\!}
值。
總結前面導引出結果,波函數
ψ
{\displaystyle \psi \,\!}
形式為:
當
x
{\displaystyle x\,\!}
趨向負無窮,包含
F
{\displaystyle F\,\!}
項目趨向。
延伸閱讀…
類,當
x
{\displaystyle x\,\!}
趨向,包含
I
{\displaystyle I\,\!}
項目趨向。
可是,波函數任何
x
{\displaystyle x\,\!}
是值。
因此,設定
F
=
I
=
0
{\displaystyle F=I=0\,\!}
。
阱外區域波函數變為
阱左邊,隨著
x
{\displaystyle x\,\!}
,波函數
ψ
1
(
x
)
{\displaystyle \psi _{1}(x)\,\!}
呈指數遞減。
而阱右邊,隨著
x
{\displaystyle x\,\!}
,波函數
ψ
3
(
x
)
{\displaystyle \psi _{3}(x)\,\!}
呈指數遞減。
這是合理。
這樣,波函數才能夠歸一化。
於方形阱稱於
x
=
0
{\displaystyle x=0\,\!}
,可以利用這稱性來省略計算步驟。
波函數不是奇函數函數。
假若,波函數
ψ
{\displaystyle \psi \,\!}
是奇函數,則
於整個波函數
ψ
{\displaystyle \psi \,\!}
滿足性可微性。
阱壁,兩個波函數函數值導數值相配:
