偏角法是一種用於平曲線測試中的方法,根據偏角和絃長來確定曲線上各點的實地位置。在測定圓曲線的主要點時,我們需要知道切線長度、曲線長度和外距,這些元素被稱為主點測定要素。使用偏角法進行測量時,第一階段通常是測量每個20米測點的偏角,即切線方向和鏡尺點到每個測點絃線之間的夾角。在移動鏡尺點之後的每個測段中,要測量鏡尺點之間的絃線和鏡尺點到每個20米測點絃線之間的夾角。對於最後一個鏡尺點,我們需要測量鏡尺點之間的絃線和切線方向的夾角。然後,既有曲線的轉角等於上述各角的總和。在主要測定點上,我們將測量儀器放置在轉向點JD上,依次瞄準兩個切線方向,沿著切線方向測量切線長度T,標定曲線的起點ZY和終點YZ。然後再對準ZY點,測量角度(180°-a)/2,得到分角線方向JD。
偏角法是用於測量平曲線上各點位置的方法,通過測量偏角和絃長,可以確定曲線上每個測點的準確位置。在實地測設圓曲線的主點時,需要先測量切線長、曲線長和外距,這些元素合稱為主點測設元素。

偏角法的實施分為兩個階段:首先,在轉向點JD安裝經緯儀,沿切線方向測量切線長T,並在ZY和YZ點標記曲線的起點和終點。然後,移動置鏡點,測量置鏡點之間的絃線和置鏡點到每個20米測點的絃線之間的夾角。最後,在最後一個置鏡點,測量置鏡點之間的絃線和切線方向的夾角。將所有這些角度相加,即得出既有曲線的轉角。
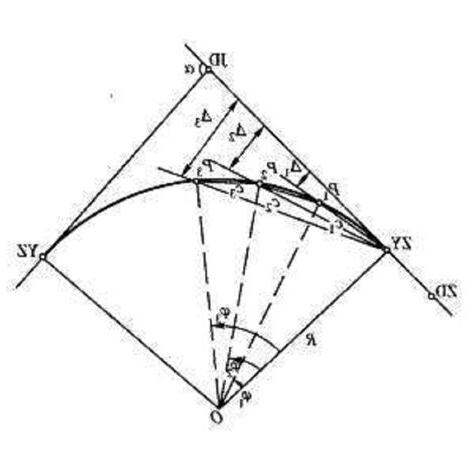
測設主點時,首先在轉向點JD安置經緯儀,沿切線方向丈量切線長T,並標定曲線的起點ZY和終點YZ。然後再照準ZY點,測設角(180°-a)/ 2,沿此方向丈量外矢距E,即得曲中點QZ。
公式a中,li是從i點到ZY點或YZ點的弧長,φi是li所對應的圓心角。在實際操作中,建議將曲線分為兩部分,以QZ為界,分別進行測設。
《工程測量實驗指導》一書是為了加強學生實際操作能力而編寫的,書中包含了20個實驗項目,這些項目都是根據《土木工程測量》課程內容設計的。這些實驗不僅覆蓋了測量理論知識,還考慮到了現有的工程測量生產實踐。通過這20個實驗項目的實踐,學生可以初步掌握工程測量中基本的儀器操作和作業流程。
書中列出了20個實驗項目的具體內容,它們既涵蓋了理論知識,也考慮了實際應用。每項實驗的目的是幫助學生理解和掌握工程測量的基本技能。
偏角法是一種在解析幾何中常用的方法,它可用於研究平面上的點、線以及形狀之間的關係。這種方法靈活且強大,常常被數學家和工程師們廣泛應用。
在偏角法中,我們將點表示為複數的形式,其中實部代表點的橫坐標,虛部代表點的縱坐標。通過將點轉換為複數,我們可以使用複數運算來簡化許多幾何問題的計算。
例如,假設有兩個點A和B,我們想計算它們之間的距離。我們可以將A和B轉換為對應的複數a和b,然後計算二者之差的絕對值,即|b-a|,即可得到它們之間的距離。
另一個偏角法的重要概念是向量的表示。以A和B為例,我們可以計算從A指向B的向量,即向量AB。這可以通過將B減去A的複數表示來實現,即b-a。
透過偏角法,我們可以進一步研究向量的性質,如向量的長度、方向、內積和外積等。這些性質在許多領域中都具有重要的應用,例如機械工程、電子學、物理學等。
總結
偏角法是一種非常有用的工具,它將解析幾何中的問題轉換為複數運算和向量計算的問題,使研究和計算更加簡便。無論您是學生還是專業人士,掌握偏角法都將對您的數學和工程學習大有裨益。
希望這篇文章對您有所幫助,如果您有任何疑問或需要進一步瞭解,請隨時向我提問!
延伸閲讀…
偏角法[確定曲線上各點在實地位置的方法] – 抖音百科
偏角法導線測量- 教育百科
