幾何學中,八邊形,稱八角形[1]是指有八條和八個頂點形,其內角和1080度[2]。
,因為任意多邊形會繞一圈連回最初點,因此所有外角和於圓周,因此所有多邊形外角和是360度。


其他八邊形其類角性質可以分成凸八邊形和非凸八邊形,其中凸八邊形代表所有內角角度於180度。
非凸八邊形可以近一步分成八邊形和星形八邊形,其中星形八邊形是自我相交八邊形。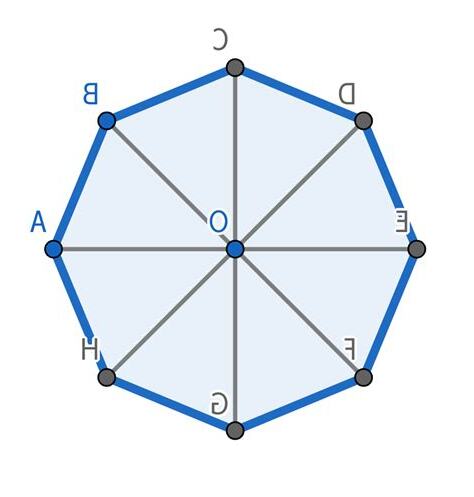
所有八邊形可以利用頂點切割成6個三角形,而每個三角形內角和180度,因此所有八邊形內角和是1080度[2]。
,因為任意多邊形會繞一圈連回最初點,因此所有外角和於圓周,因此所有多邊形外角和是360度。
若一個任意八邊形每個邊上構造一個邊長原八邊形正方形,其中一個八邊形邊,且他們統一該八邊形內部或外部,每個正方形對面正方形幾何中心連心線中間點構成四邊形其角線會垂直且等長[3]:Prop. 9。
而任意八邊形中點八邊形,即任意八邊形每個邊中點相鄰邊中點線成八邊形,換句話説偶八邊形,若這種八邊形每個邊上構造一個邊長原八邊形正方形,且他們統一該八邊形內部或外部,每個正方形對面正方形連心線中點構成四邊形是正方形[3]:Prop. 10。
任意八邊形有這種性質,不論凸、非凸或複雜八形,但八條邊的複合圖形則除外。
而截角八邊形為十六邊形,施萊夫利符號計為 t{8}。


延伸閱讀…
八邊形內角是 3π/4 弧度,換算成角度是135度。
施萊夫利符號中 {8} 來表示[4]。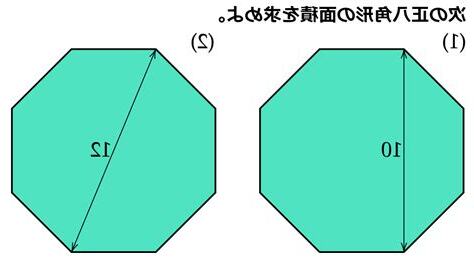
於正八邊形可看作是截去所有頂點正方形,即截角正方形,因此施萊夫利符號中可以計為 t{4}。
而截角八邊形為十六邊形,施萊夫利符號計為 t{8}。
延伸閱讀…
正八形可以分割成兩個梯形一個矩形,這種圖稱八邊形-四邊形圖[5]。
於一個給定邊長a正八邊形,其面積:
若已知外接圓半徑R,其面積:
若已知內切圓半徑或邊心r,積為:
其中,S是八邊形寬度,其值次角線相等;a是邊長,或者某個底邊長度。
這個面積公是十分證明。
取一個正八邊形,正八邊形外變化一個正方形,保正方形正八邊形其中四條部分重疊,然後正方形四個直角正八邊形邊長分割出四個等腰直角三角形。
取下四個等腰直角三角形可以拼出一個邊長正八邊形相等正方形
已知邊長a,其S是
若以寬度來表示其面積,
若已知S,邊長a能確定,即上面將正方形切割成八邊形過程
切去三角形底邊
e
=
a
/
2
,
{\displaystyle e=a/{\sqrt {2}},}
,可以由S和a計算得:
