在幾何學中,六邊形是指有六條邊和六個頂點的多邊形,其內角和為720度。六邊形有很多種,其中對稱性最高的是正六邊形。正六邊形是一種可以使用尺規作圖的六邊形,也可以拼滿平面,因此自然界中可以找到許多正六邊形的結構,如蜂巢、玄武岩和苯的分子結構。另外,正六邊形也可以構成一些高對稱性的多面體,如截角二十面體,巴克明斯特富勒烯的分子結構就是這種形狀。
六邊形依照其類角的性質可以分成凸六邊形和非凸六邊形,其中凸六邊形代表所有內角的角度皆小於180度。非凸六邊形可以在近一步分成凹六邊形和星形六邊形,其中星形六邊形表示邊自我相交的六邊形。
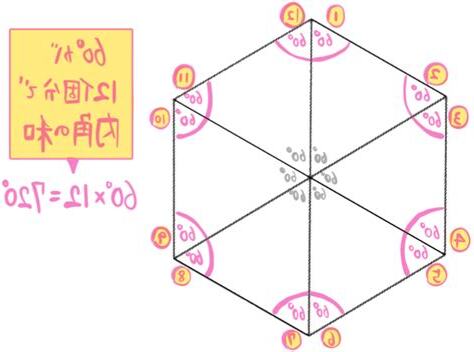
正六邊形是每條邊等長、每個角相等的六邊形,六角形內角和是720度。


正六邊形:幾何中的基本多邊形
在幾何學中,正六邊形是一個具有六條邊和六個頂點的多邊形,每個內角為120度,且每個邊長都相等。根據施萊夫利符號,正六邊形可以表示為{6},並且具有6次旋轉對稱性和6軸對稱性,構成了D6二面體的對稱性。正六邊形的邊長與其外接圓半徑相等,且每個內角都是120度。
正六邊形的構造
正六邊形可以通過將正三角形進行截角變換來構造,即切去正三角形的三個頂點。這一過程會產生一個具有邊可遞和點可遞特性的六邊形,並且是一個雙心多邊形,即同時具有內切圓和外接圓。此外,正六邊形的邊長與其外接圓半徑相等,且邊心距與內切圓半徑相等。
正六邊形的對稱性
正六邊形具有6次旋轉對稱性和6軸對稱性,組成了D6二面體羣的對稱性。正六邊形最長的對角線是兩側頂點之間的對角線,其長度恰好為邊長的兩倍。在正面體羣中,正六邊形是其中一種能夠密鋪平面的正多邊形,與正三角形和正方形一起,可以經過重複的排列和組合,形成沒有空隙或重疊的幾何圖形,有效地利用空間和建材。
正六邊形的應用
正六邊形的對稱性和密鋪特性使其在自然界中很常見,例如在蜂巢中,每個蜂房的形狀都是正六邊形,這可以有效利用空間和建材。此外,正六邊形也是一些分子結構的基礎,如苯的分子結構就是一個由正六邊形構成的環狀結構。在幾何學中,正六邊形是一個基礎的多邊形,其特性和應用在許多科學領域中都很重要。
正六邊形在幾何學中佔有重要位置,不僅因為它是正多邊形的一種,還因為它在自然界中頻繁出現,並且在建築、工藝和化學結構中都有應用。
|
正六邊形是一個邊長相等、內角為120度的六邊形。 |
正六邊形的邊長與外接圓半徑相等,且內角為120度。 |
|
正六邊形通過將正三角形進行截角變換來構造,從而獲得邊可遞和點可遞特性。 |
正六邊形的邊心距與內切圓半徑相等,且最長對角線是邊長的兩倍。 |
正六邊形能夠密鋪平面,並且在自然界的蜂巢、岩石結構以及一些分子結構中都有所體現。
六角形是一種幾何形狀,它具有六個邊和六個角。
你知道嗎?六角形的內角和是720度。
「六角形內角和」這個詞組可以用來描述這個幾何形狀中所有內角的總和。
要計算六角形內角和,我們可以使用一個簡單的公式:
內角和 = (六邊形的邊數 – 2) × 180度
將這個公式應用於六角形,我們可以得到:
六角形內角和 = (6 – 2) × 180度 = 4 × 180度 = 720度
這就是為什麼六角形內角和永遠是720度的原因。
六角形內角和的這個特性使得它在許多數學和科學應用中非常有用。
有趣的是,六角形也是自然界中許多物體的基本形狀。
蜜蜂巢穴、冰雪結晶、某些花朵的排列方式,甚至一些行星上的撞擊坑,都可以見到六角形的存在。
這些自然界中的六角形相關現象是非常有趣且美麗的,也給了科學家和數學家很多研究的材料。
總結來説,六角形內角和是非常重要和有趣的數學概念。
它幫助我們理解六角形的特性,並在各個領域中有廣泛的應用。
無論是在數學的課堂上還是在日常生活中,我們都可以看到六角形內角和的存在。
延伸閲讀…
六邊形
六邊形_百度百科
希望這篇文章能讓你對這個主題有更深入的理解。
