凹形 多邊形 、凹形 多邊形 或非凸 多邊形 、非凸 多邊形 ,多面體與多胞體亦然。
凸 數多胞形。
凹數多胞形。
在幾何學中,一個幾何圖形可分為凸或凹的。例如多邊形和多面體。其中,凸的多邊形稱為凸多邊形、凹的多邊形則可稱為凹多邊形或非凸多邊形,多面體與多胞體亦然。然而在三維或更高維度的空間中,不是凸的幾何圖形不一定會是凹幾何圖形,亦可能是星形幾何圖形,因此在三維或更高維度的空間中較常分為凸與非凸。


|
凸幾何圖形是指內部為凸集的幾何圖形[1],二維空間中的凸幾何圖形稱為凸多邊形、三維空間則稱凸多面體。若一多胞形的內部為凸集,則稱凸多胞形。 |
二維空間中的凸幾何圖形稱為凸多邊形,簡單多邊形的下列性質與其凸性等價:
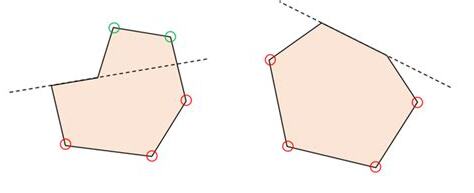
凹幾何圖形是指內部不是凸集的幾何圖形,在二維空間中,不是凸集的簡單多邊形,稱為凹多邊形(Concave polygon)[2]或凹角[3]。
凹多邊形是幾何學的名詞,為多邊形分類中的一類。其特徵為至少有一個內角介於180∘與360∘之間(這種角又稱作優角)[1]。注意上述的內角角度不包含180∘與360∘,因為會屬於另外一種多邊形——退化多邊形。
簡單多邊形是其任何邊都不會與自身相交的多邊形,而簡單多邊形可以根據凹凸性再分成凸多邊形(英語:convex polygon)與凹多邊形(英語:concave polygon)兩類。
初等幾何學與幾何學對於凹多邊形的定義有所差異。初等幾何學只討論在簡單多邊形當中的凹多邊形,如前一小節所述。
Georg Jensen 純銀凹形器皿。我們在這裏包含許多不同的商品。這包括 Georg Jensen 品牌和 Johan Rohde 的早期新藝術運動設計。也包括西格瓦德-貝納多特、哈拉爾-尼爾森的裝飾藝術設計,或者亨寧-科佩爾、馬格努斯-斯蒂芬森和 Bluitgen的現代設計。我們有大量的咖啡用具,茶具、盤子、碗、蓋子碗、陶器、杯子、花瓶、燭台、魚盤、蓋盤、酒吧設備、雞尾酒調酒器、信刀、水壺、鹽和胡椒罐、糖罐、藥盒、箱子;我們這裏有很多商品的選擇,而且包含純銀,826 以及 830 銀的材質。
凹形是一種幾何形狀,它有一個凹陷的外形。它可以在各種物體中找到,例如凹陷的碗、凹陷的鏡子等。這種形狀通常給人一種深邃和神秘的感覺。
一個常見的例子是凹鏡,它是一種具有透鏡效果的凹形物件。凹鏡會使經過的光線彎曲,並最終聚焦到一個點上。這種特性使得凹鏡在光學實驗和眼鏡製造中被廣泛使用。
除了光學應用外,「凹形」也在設計和藝術領域中扮演了重要的角色。設計師常常使用凹形來創造出獨特且引人入勝的視覺效果。例如,室內設計師可能會使用凹形的壁爐來營造出一個温馨和舒適的氛圍,而街頭藝術家則可能使用凹形的圖案來吸引行人的注意。
此外,「凹形」也可以在自然界中找到。例如,一些魚類的身體形狀是凹形的,這使它們能夠更有效地遊動。同樣地,一些植物的葉子也具有凹形,這有助於它們收集更多的陽光並進行光合作用。
總而言之,「凹形」是一個多功能的形狀,它在各個領域都發揮著重要作用。不論是在科學、設計還是自然界中,我們都可以找到凹形的存在。透過適當的應用,凹形可以帶來不同的效果和體驗。
希望這篇文章能為您帶來一些關於「凹形」的新見解!
延伸閲讀…
雙凹形
凹多邊形
