泰勒斯定理
泰勒斯定理揭示了幾何中一個著名的性質。此定理指出,在半徑為r的圓內,假設A、B、C三點位於圓週上,且AC為圓的直徑,則∠ABC為直角。換句話説,直角三角形的斜邊長等於圓的直徑。
證明:

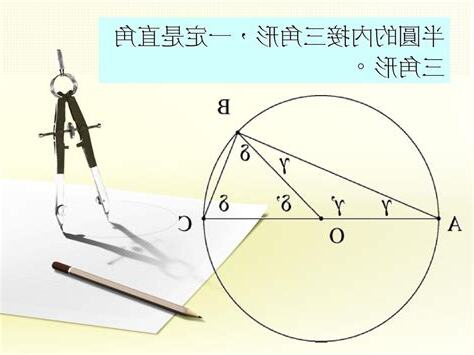
設圓心為O,連結OA、OB、OC。
- 根據等腰三角形的性質,∠OBC = ∠OCB,∠BAO = ∠ABO。
-
將此連同∠ABC為180°代入,得到:
- ∠OBC + ∠OCB + ∠OBC = 90°
- ∠BAO + ∠ABO + ∠BAC = 90°
-
因此,∠ABC = 90°,證明瞭泰勒斯定理。
逆定理:
泰勒斯定理的逆定理也成立,即:直角三角形中,直角的頂點位於以斜邊為直徑的圓上。
數學證明:
設O為圓心,∠ABC = 90°。
- OA = OB(半徑相等)
- 根據等腰三角形性質,∠OBC = ∠OCB
-
由於∠ABC = 90°,因此:
- ∠OBC + ∠CBA = 90°
- ∠OBC + ∠OCB = 90°
-
兩條等式相加,得出:
- 2∠OBC = 180°
- ∠OBC = 90°
-
因此,BC與OA垂直。同理可證,AC與OB垂直。
結論:
泰勒斯定理和其逆定理在幾何學中具有重要的意義。它們為理解圓、三角形和其他幾何形狀的性質提供了基本框架。
半圓內接三角形
半圓內接三角形是其直角點位於半圓上、其他兩頂點位於半圓內的三角形。本篇文章將探討半圓內接三角形的基本性質、公式和應用。
性質
- 半圓半徑為三角形外接圓半徑的兩倍。
- 半圓內接三角形的直角邊為外接圓弦。
- 半圓內接三角形的斜邊為外接圓的直徑。
公式
| 性質 | 公式 |
|---|---|
| 外接圓半徑 | R = 2r |
| 直角邊長度 | a = b = r√2 |
| 斜邊長度 | c = 2r |
| 面積 | A = (1/2)r² |
| 外切圓半徑 | R = r |
證明
證明 1:外接圓半徑
由於半圓的直徑等於三角形的斜邊,因此外接圓半徑(R)為半圓半徑(r)的兩倍。
證明 2:直角邊長度
根據畢氏定理,直角邊長度(a)平方 ditambah 斜邊長度(c)平方 等於外接圓半徑(R)平方。由於斜邊長度為 2r,因此:
a² + b² = R²
a² + b² = (2r)²
a² = b² = r² × 2
a = b = r√2
應用
半圓內接三角形廣泛用於數學、物理和工程等領域中,包括:
延伸閲讀…
泰勒斯定理
【觀念】半圓所對的圓周角| 數學
- 三角函數:計算特定角度的正弦、餘弦和正切值。
- 距離測量:使用相似三角形原理測量難以到達的距離。
- 弧度計算:將圓周率與圓周長或半徑聯繫起來的度量單位。
- 車輛設計:用於計算汽車懸吊系統中的懸吊行程和輪胎接地面積。
總結
半圓內接三角形是一種重要的幾何形狀,具有獨特的性質和公式。瞭解這些性質和公式對於解決各種與半圓和三角形相關的問題至關重要,有助於我們深入理解數學和物理等領域的原理。
