圓形有時叫圓,係圓嘅幾何圖形。圓形個中心叫圓心,而條邊嘅叫圓周。圓心同圓周之間,每點嘅直綫距離係一樣嘅,呢個距離就叫半徑。而一條直綫,由一圓週上一點,通過圓心到圓周另一邊,呢個就叫直徑。
喺圓形上面任意篤兩點,然後用直線連埋,嗰條直線就叫做弦。將條弦向兩邊延長,就變咗做割線。如果一條直線同圓形只有一個交點,嗰條直線就叫做切線。圓周嘅一橛仔就係弧。弧嘅兩邊同兩條半徑組成扇形,而弧嘅兩邊同弦組成弓形。

圓的中心點叫什麼圓心,圓的中心點叫什麼圓心。
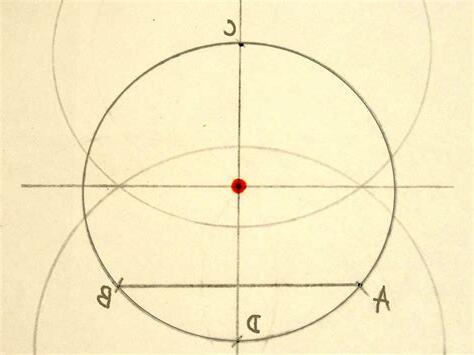
圓形係點樣定義嘅?
圓形嘅中心點同邊界有乜關係?
每點嘅直綫距離係一樣嘅,呢個距離就叫半徑。
點樣量度圓形嘅大細?
可以用半徑嘅長度嚟量度。
咩係圓形的幾何特性?
圓形有好多幾何特性(定理),例如:
- 所有喺圓形上嘅點嘅半徑都係一樣長。
- 任何一條過圓心嘅直線都會平分經過嗰個點嘅弦。
圓是幾何中的一個基本形狀,它由一組所有點到圓心距離相等的點組成。圓的中心點是整個圓的核心,它擁有特殊的性質和重要的地位。讓我們深入探討一下圓心的特點及其在幾何中的作用。
圓心的特點
圓的中心點有幾個重要特點:
- 唯一性:每個圓只有一個圓心,它是圓的獨特標誌。
- 對稱性:圓心對圓上的每一點都具有對稱性,也就是説,從圓心到圓上的任何一點的線段都可以被視為圓的直徑,並且通過圓心的對稱軸將圓分成兩個相等的部分。
- 到圓上各點的距離相等:這是圓心最重要的特點,也是定義圓的關鍵性質。從圓心到圓上的任何一點的距離都相等,這個距離被稱為半徑。
圓心在幾何中的作用
圓心在幾何中扮演著非常重要的角色,應用廣泛:
