材料力學是所有力學考科如結構學、鋼鐵混凝土設計的根基,其公式推導涉及假設前提和概念,可提升觀念和理解三大原則。解題技巧固然重要,但理解材料力學對所有科目皆有益處,尤其結構技師考生的題目難度較高,熟練推導有助於解難。
深入瞭解公式推導有助於背誦和提升素養,與口訣搭配使用能事半功倍。
截面面積(A)、位移(y)、慣性矩(I)等幾何和力學特徵用於驗算構件截面的承載力和剛度。


【範例】已知二跨等跨梁,均布荷載和集中荷載如下,求中間支座的最大彎矩和剪力。
【範例】已知三跨等跨梁,均布荷載如下,求邊跨最大跨中彎矩。
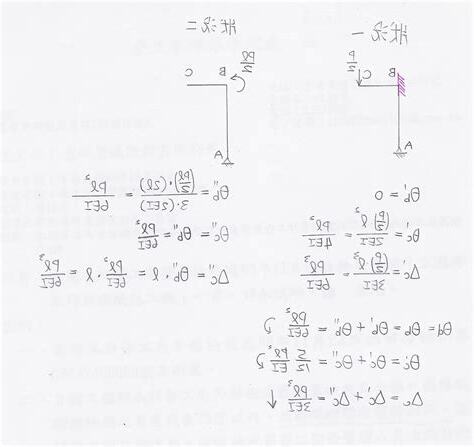
簡支與固定的邊界條件有四種:
| 邊界條件 | 紅色虛線表示的邊界條件 |
|---|---|
| 三邊簡支,一邊固定 | 一邊固定 |
| 兩邊簡支,兩邊固定 | 兩邊固定 |
| 一邊簡支,三邊固定 | 三邊固定 |
| 兩邊簡支,兩邊固定 | 兩邊固定 |
對於矩形等寬度實腹式變截面拱,公式 I=Ic/cos(θ) 與截面面積變化公式具有相同的規律。
基本變位公式口訣:加、減、乘、除,變形不變
基本變位公式,是數學中用於變形方程式的基本公式口訣,其口訣為:
加、減同號變等號,乘除同號變等號
加、減異號變減號,乘除異號變負號
透過這個口訣,我們可以快速判定在變位運算後方程式的符號。
加法與減法
| 運算 | 結果 |
|---|---|
| 加法 + + | 等號 = |
| 減法 – – | 等號 = |
| 加減 + – | 減號 – |
| 減加 – + | 減號 – |
乘法與除法
| 運算 | 結果 |
|---|---|
| 乘法 * * | 等號 = |
| 除法 / / | 等號 = |
| 乘除 * / | 負號 – |
| 除乘 / * | 負號 – |
應用範例
假設我們有一個方程式:
$$ x + 5 = 10 $$
我們想把 x 變成主詞,可以使用 加 運算:
$$ x + 5 - 5 = 10 - 5 $$
根據 加異號變減號 準則,+5 和 -5 是異號,因此變成減號:
$$ x = 5 $$
分數變整數
在應用這個口訣時,需要將分數先化成整數。常用的方法有:
含有 0 的加法和減法
| 運算 | 結果 |
|---|---|
| 分子為 0 + 0 | 無意義 |
| 分子為 0 – 0 | 無意義 |
| 分母為 0 + 分數 | 無意義 |
| 分母為 0 – 分數 | 無意義 |
含有 0 的乘法和除法
| 運算 | 結果 |
|---|---|
| 分子或分母為 0 * 0 | 0 |
| 分子為 0 * 非 0 | 0 |
| 分母為 0 * 非 0 | 無意義 |
| 分子為 0 / 非 0 | 0 |
| 分母為 0 / 非 0 | 無意義 |
