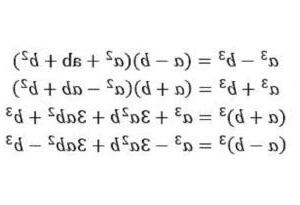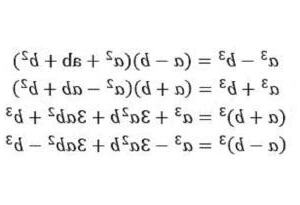在數學中,完全立方是一個數,當它被自乘三次時,其結果是一個整數,而且這個整數可以分解為三個相同的因子的乘積,例如125 = 5 × 5 × 5,因為125是5的一個完全立方。然而,對於某些數字,如1331,雖然1331 = 11 × 11 × 11,但它不是一個完全立方,因為11不是一個完全平方數。完全立方的概念在數學中有著廣泛的應用,特別是在代數幾何和數論中。
隨著科技的進步,完全立方數的研究也在不斷推
完全立方和與差公式
完全立方和與差公式是用來解決涉及立方和或差的多項式計算問題的兩種方法。這些公式在數學中非常重要,尤其是在解方程和進行代數運算時。以下是這兩個公式的簡要説明:
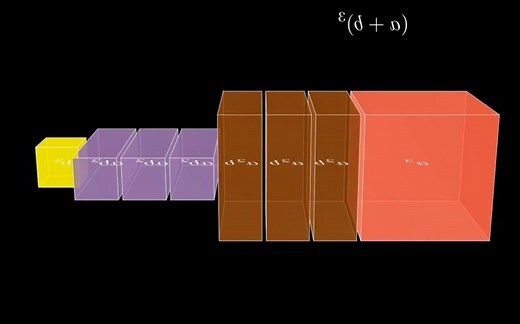
1. 完全立方和公式
(a + b)^3 = a^3 + 3a^2b + 3ab^2 + b^3
這個公式用來計算兩個數字a和b的立方和。公式中的每一項都是由a和b的不同組合組成的。例如,第一項a^3是a的立方,而第二項3a^2b是a的平方乘以b。這個公式的結構特徵是左邊是兩個相同的項相乘,右邊是三項式,其中包含了左邊項目的立方和、平方和以及乘積。
2. 完全立方差公式
(a – b)^3 = a^3 – 3a^2b + 3ab^2 – b^3
這個公式用來計算兩個數字a和b的立方差。公式中的每一項都是由a和b的不同組合組成的。例如,第一項a^3是a的立方,而第二項3a^2b是a的平方乘以b。這個公式的結構特徵是左邊是兩個相同的項相乘,右邊是三項式,其中包含了左邊項目的立方差、平方差以及乘積。
在應用這兩個公式時,需要注意公式的正確應用條件,並且要小心不要遺漏任何一項。此外,如果多項式中含有其他項,可能需要將這些項先進行因式分解,以便應用完全立方和




延伸閲讀…
延伸閲讀…