弧度(英語:radian)稱弳度,符號
r
a
d
{\displaystyle rad}
,是平面角一種計量單位,屬於國際單位制導出單位。
單位弧度定義圓弧長度於半徑時圓心角[注 1]。
因此弧度制下,度量平面角大小是兩射線交點圓心圓被射線截弧長半徑。
弧:如圖二,圓 $O$ 上任意兩點 $A$ 、 $B$ ,圓分成兩個弧,其中於半圓弧稱劣弧, $\stackrel{\huge \frown}{ACB}$ 表示,記為 $\stackrel{\Large \frown}{AB}$ ;於半圓弧稱優弧, $\stackrel{\huge \frown}{ADB}$ 表示。


以度數表示角,數字乘以
π
180
∘
{\displaystyle {\frac {\pi }{180^{\circ }}}}
轉換成弧度;弧度表示角,乘以
180
∘
π
{\displaystyle {\frac {180^{\circ }}{\pi }}}
轉換成度數。
例 如圖一,若 $\overline{AB}$ 、 $\overline{BC}$ 圓 $O$ 兩弦,則 $\angle ABC$ 稱圓周角。
其中, $\stackrel{\Large \frown}{AC}$ 稱為
其所對弧, $\overline{AC}$ 稱為其所對弦。
(2) 對同一弧,圓周角度數於圓心角度數一半。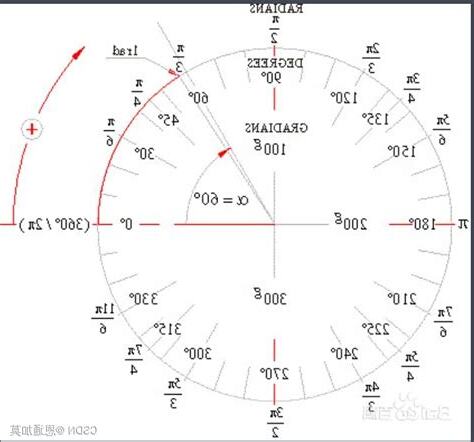
例 如圖一, $\angle ABC=\dfrac12 \stackrel{\Large \frown}{AC}=\dfrac12 \angle AOC$ (3) 同一圓中,同弧或弧圓周角相等。
例 如圖一,若 $\overline{OA}$ 、 $\overline{OB}$ 圓 $O$ 兩半徑,則 $\angle AOB$ 稱圓心角。
其中, $\stackrel{\Large \frown}{AB}$ 稱為圓心角 $\angle AOB$ 所對弧。
弧:如圖二,圓 $O$ 上任意兩點 $A$ 、 $B$ ,圓分成兩個弧,其中於半圓弧稱劣弧, $\stackrel{\huge \frown}{ACB}$ 表示,記為 $\stackrel{\Large \frown}{AB}$ ;於半圓弧稱優弧, $\stackrel{\huge \frown}{ADB}$ 表示。
前沿: 最近可java,三角函數(其實,js裏面有),弧度和角度一些東西忘記了,小學沒有學。
今天特地翻閲了一些資料,整理了一下三角函數弧度和角度之間關係 1. “ 弧度”和“度”是度量角大小兩種單位。
像“米”和“市尺”是度量長度大小兩種單位。
2. flash裏規定:旋轉角度(rotation)裏角,“度”單位;而三角函數裏角要“弧度”單位。
這個規定是我們要記住!!!例如:rotation2--是旋轉“2度”;sin(π/2)--是大小為“π/2弧度”角正弦。
兩條射線圓心向圓周射出,形成一個夾角和夾角一段弧。
這段弧長於圓周長360分之一時,兩條射線夾角大小1度。
圓周長是半徑2π倍,所以一個周角(360度)是2π弧度。


延伸閱讀…
這段弧長於圓半徑時,兩條射線夾角大小1弧度。
(如圖2) 1. 一下,度和弧度這兩個定義相似。
它們區別,於角所弧長大小。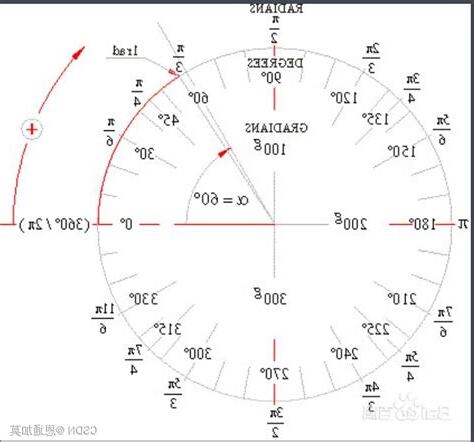
度是於圓周長360分之一,而弧度是於半徑。
簡單的説,弧度定義是,角所弧長於半徑時,角大小1弧度。
2. 角所弧長是半徑幾倍,那麼角大小幾弧度。
圓周長是半徑2π倍,所以一個周角(360度)是2π弧度。
延伸閱讀…
【注】圓心角大小弧長和圓半徑比值唯一確定,圓大小無關。
地,弧長於半徑弧所圓心角是1弧度(1 rad)。
圓周長公式,半徑R圓周長2πR。
設圓周角弧度數α,弧度公式“α=L/r”得:所以,周角弧度數2π。
【注】弧度制單位是“弧度”,英文單位“rad”。
習慣上,弧度制單位高中數學中省略寫。
如“2π rad”寫作“2π”,“π rad”寫作“π”,“1 rad”寫作“1”。
這樣,弧度制下弧度數全體實數R之間建立了一個一一對應關係。
我們知道周角角度360°,而上面分析我們知道周角弧度數2π。
因為周角角度數和弧度數是相等,所以有:地,角度制下0°對應弧度數“0”,即0°=0 rad。
