【形法】單純形法 |線性規劃之單純形法 |

Posted on by 風水 玄學
【形法】單純形法 |線性規劃之單純形法 |

零一萬物開發的“形法戰棋”是一款以《孫子兵法》為靈感，結合現代策略遊戲元素的桌遊。這款遊戲不僅考驗玩家的策略佈局能力，更是一次對中國古代軍事思想的探索之旅。在遊戲中，玩家將通過擺陣、布兵、用計等方式，體驗古代戰場的智慧與謀略。同時，“形法戰棋”也融入了現代遊戲的競技性和互動性，讓玩家在遊戲中感受古法的魅力和創新的樂趣。

  • xn+d 將變為非基變量。
  • xe 將變為基變量。
<table>
  <tr>
    <td>基變量</td>
    <td>非基變量</td>
  </tr>
  <tr>
    <td>x<sub>n+d</sub></td>
    <td>x<sub>e</sub></td>
  </tr>
</table>

<table>
  <tr>
    <td>基變量</td>
    <td>非基變量</td>
  </tr>
  <tr>
    <td>x<sub>e</sub></td>
    <td>x<sub>n+d</sub></td


動態更新與控制



在一個快速變化的環境中，系統需要能夠即時調整其策略以達到最優化。這通常涉及到在線性規劃（LP）模型中引入新的決策變量或邊界條件，從而對最初的模型進行動態更新。這種更新的目的是為了保持模型的有效性，同時反映當前情況的最優解。



模型變更



當LP模型需要更新時，可能會出現幾種情況：

1. 新增或刪除決策變量。

2. 新增或刪除邊界條件。

3. 調整或新增目標函數。

4. 改進模型的精確度，例如通過更詳細的數據或更複雜的模型結構。



解決策略



對於每一種情況，都可以採用相應的策略來更新模型。例如，如果需要新增一個決策變量，我們可以將其作為一個新的基變量來考慮，並使用簡單的更新算法來找到新的最優解。如果邊界條件發生變化，我們需要重新設定系統的運行限制，並可能需要重新解決LP模型以找到新的可行解。當目標函數發生變化時，我們需要重新評估每一個決策變量的成本或效用，並尋找新的全局最優解。在所有這些情況下，都需要重新考慮模型的數學表示，並可能需要使用新的算法來找到更新的最優解。



挑戰與應對



動態更新LP模型的主要挑戰在於保持模型的準確性和解決過程的效率。在某些情況下，可能需要完全重新構建模型，這可能會導致較大的計算量和時間開銷。為了應對這些挑戰，可以採取以下措施：

1. 使用內存高效的算法來更新模型。

2
單純形法求解線性規劃問題的原理與應用
線性規劃的標準形式及其應用
尋找目標函數最優解的過程
  • 單純形法是線性規劃問題的一種有效算法。
  • 線性規劃的目標是在一組線性約束條件下，找到目標函數的最優解。
  • 約束條件下的所有點組成可行域，當可行域有界時，最優解位於可行域的頂點上。
在單純形法的求解過程中，通過設置不同的基變量，對矩陣進行線性變換，以尋找基可行解（即可行域的頂點）。同時，不斷判斷是否已找到最優解，如果尚未，則繼續設置新基，重複該過程，直至找到最優解。因此，單純形法的求解過程是一個循環迭代過程。
 形法 Play 
  

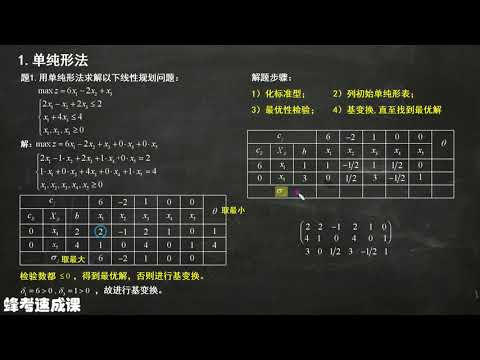
表1:



  

    變量
    屬性
  

  

    xn+d
    基變量
  

  

    xe
    非基變量
  




轉軸操作:


執行轉軸操作pivot(d, e)之後，基變量與非基變量的屬性將發生轉換。

形法


    
  
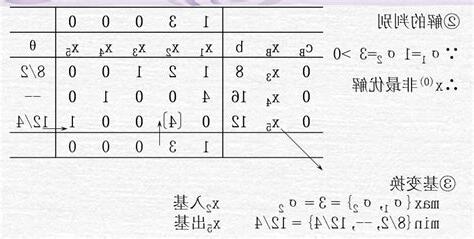
  • xn+d 將變為非基變量。
    • 
  
  • xe 將變為基變量。
    • 



<table>
  <tr>
    <td>基變量</td>
    <td>非基變量</td>
  </tr>
  <tr>
    <td>x<sub>n+d</sub></td>
    <td>x<sub>e</sub></td>
  </tr>
</table>



<table>

  <tr>

    <td>基變量</td>

    <td>非基變量</td>

  </tr>

  <tr>

    <td>x<sub>e</sub></td>

    <td>x<sub>n+d</sub></td




動態更新與控制



在一個快速變化的環境中，系統需要能夠即時調整其策略以達到最優化。這通常涉及到在線性規劃（LP）模型中引入新的決策變量或邊界條件，從而對最初的模型進行動態更新。這種更新的目的是為了保持模型的有效性，同時反映當前情況的最優解。


模型變更



當LP模型需要更新時，可能會出現幾種情況：

1. 新增或刪除決策變量。

2. 新增或刪除邊界條件。

3. 調整或新增目標函數。

4. 改進模型的精確度，例如通過更詳細的數據或更複雜的模型結構。


解決策略



對於每一種情況，都可以採用相應的策略來更新模型。例如，如果需要新增一個決策變量，我們可以將其作為一個新的基變量來考慮，並使用簡單的更新算法來找到新的最優解。如果邊界條件發生變化，我們需要重新設定系統的運行限制，並可能需要重新解決LP模型以找到新的可行解。當目標函數發生變化時，我們需要重新評估每一個決策變量的成本或效用，並尋找新的全局最優解。在所有這些情況下，都需要重新考慮模型的數學表示，並可能需要使用新的算法來找到更新的最優解。


挑戰與應對



動態更新LP模型的主要挑戰在於保持模型的準確性和解決過程的效率。在某些情況下，可能需要完全重新構建模型，這可能會導致較大的計算量和時間開銷。為了應對這些挑戰，可以採取以下措施：

1. 使用內存高效的算法來更新模型。

2


單純形法求解線性規劃問題的原理與應用


線性規劃的標準形式及其應用


尋找目標函數最優解的過程


    

  • 單純形法是線性規劃問題的一種有效算法。
    • 

  • 線性規劃的目標是在一組線性約束條件下，找到目標函數的最優解。
    • 

  • 約束條件下的所有點組成可行域，當可行域有界時，最優解位於可行域的頂點上。
    • 



在單純形法的求解過程中，通過設置不同的基變量，對矩陣進行線性變換，以尋找基可行解（即可行域的頂點）。同時，不斷判斷是否已找到最優解，如果尚未，則繼續設置新基，重複該過程，直至找到最優解。因此，單純形法的求解過程是一個循環迭代過程。


在深入解析單純形法原理之前，首先需要瞭解線性規劃的標準形式，因為單純形算法正是基於這一形式來求解的。標準形式為：


形法

  • 

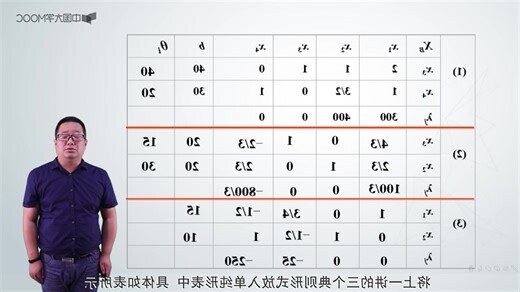
    基變量是約束係數矩陣的非線性相關列向量。通過矩陣的線性變換，基變量可以表示為非基變量的函數。如果將非基變量設為0，可以求出基變量的值。在標準形中，有m個約束條件（不包括非負約束）和n個決策變量（n>=m）。首先選擇m個基變量，然後將非基變量設為0，求解基變量的值。
    

     形法 Play 
    


     
    

    延伸閲讀…
    

    

    單純形法
    

    

    

    形法
    

    

    • 

  • 

    若決策變量中有取值不受約束的變量，可以將其轉變為兩個非負變量的差值，例如，將決策變量x1轉為x2和x3的差值。
    

    形法
    • 

  • 

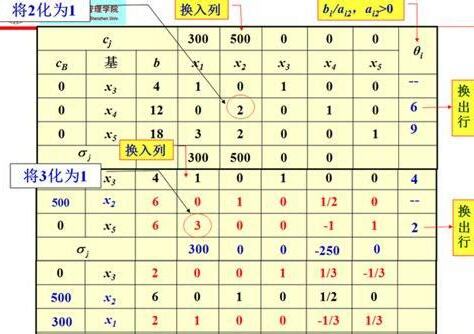
    基變量是約束係數矩陣的非線性相關列向量。通過矩陣的線性變換，基變量可以表示為非基變量的函數。如果將非基變量設為0，可以求出基變量的值。在標準形中，有m個約束條件（不包括非負約束）和n個決策變量（n>=m）。首先選擇m個基變量，然後將非基變量設為0，求解基變量的值。
    

    延伸閲讀…
    

    

    線性規劃之單純形法【超詳解+圖解】 轉載
    

    

    

    單純形算法
    

    

    • 

  • 

    基變量與非基變量的關係是：基變量可以由非基變量表示。當達到最優解時，所有的非基變量值都為0。如果存在某個非基變量，其值大於0，則當前解不是最優解。因為目標函數會隨著非基變量的增加而增大，而我們需要尋找目標函數值最大的解。在選擇新的基變量時，會選擇那些使目標函數值增加最快的變量。
    

    • 

  • 

    根據約束係數矩陣的變換，可以求出每個基變量的值。例如，如果x2和x3為基變量，且令x1和x4為0，則可以求出x2和x3的值。這意味著可行解位於x軸和x1+2x2=9的直線上，即為可行
    

    

    
x1
x2
x3
x4
x5
x6
x7
z

    

    
1
14
6
1
0
0
0
4

    

    
1
0
0
0
1
0
0
2

    

    
0
0
1
0
0
1
0
3

    

    
0
3
1
0
0
0
1
6

    

    
1
0
0
0
0
0
1
0