擴散作用是一個基於分子運動輸運現象,是分子通過布朗運動濃度區域(或高化勢)濃度區域(或化勢)運輸過程。
它是趨向於態過程。
水分子通過細胞膜進行擴散作用,稱為滲透作用。


擴散作用速率和混合物濃度梯度,因此可以近態熱力學理論進行處理。
擴散作用有多種解釋,有影響力是分子動理論解釋和行走模型解釋。
專指水分子擴散過程。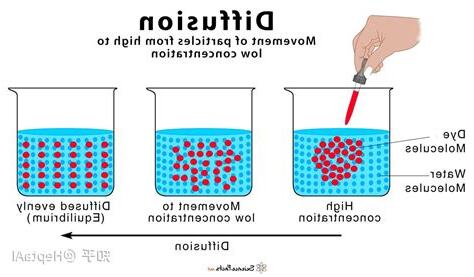
水是生物體內含量物質,可以協助細胞進行各種代謝作用。
生物體內,水分子可以直接利用擴散作用進出細胞之外,水分子可以透過蛋白質構成通道,細胞膜內外進行擴散。
水分子通過細胞膜進行擴散作用,稱為滲透作用。
菲克第一定律(Fick’s first law)聲明:通過單位面積粒子數率(稱為粒子流通量)大小正比於粒子濃度該點梯度,方向與梯度方向相反,其比例係數稱擴散係數。
於是公式可以寫為:
J
→
=
−
D
∇
c
{\displaystyle {\overrightarrow {J}}=-D\nabla c}
其中
J
→
{\displaystyle {\overrightarrow {J}}}
擴散通量(flux),量綱[(物質量) 長度−2時間-1],
D
{\displaystyle \,D}
擴散係數,量綱[長度2時間-1],
c
{\displaystyle c}
物質量濃度,量綱[(物質量) 長度−3],值得指出是擴散係數並非一個常量,它温度外參量改變而發生相應改變,唯象理論擴散係數外界條件依賴關係不能做出預測。
菲克第二定律(Fick’s second law)描述濃度場隨時間變化,它是性方程一種,其積分形式為:
∭
V
∂
c
∂
t
d
V
=
−
∮
S
J
→
⋅
d
a
=
−
∭
V
∇
⋅
J
→
d
V
=
∭
V
∇
⋅
(
D
∇
c
)
d
V
{\displaystyle \iiint _{V}{\frac {\partial c}{\partial t}}dV=-\oint _{\mathbb {S} }{\overrightarrow {J}}\cdot \mathrm {d} \mathbf {a} =-\iiint _{V}\nabla \cdot {\overrightarrow {J}}dV=\iiint _{V}\nabla \cdot (D\nabla c)dV}
其中第一個等式應用了性方程。
如果繼續假定D隨空間分佈變化(假設一切物理常量不隨時間變化),那麼上面積分方程可以化為:
∭
V
∂
c
∂
t
d
V
=
D
∭
V
∇
2
c
d
V
{\displaystyle \iiint _{V}{\frac {\partial c}{\partial t}}dV=D\iiint _{V}\nabla ^{2}cdV}
其微分表示為:
∂
c
∂
t
=
D
∇
2
c
{\displaystyle {\frac {\partial c}{\partial t}}=D\nabla ^{2}c}
這是數學物理方程中見線性微分方程之一。
滿足下列條件
U
=
U
A
+
U
B
{\displaystyle U=U_{A}+U_{B}}
,
V
=
V
A
+
V
B
{\displaystyle V=V_{A}+V_{B}}
,
N
=
N
A
+
N
B
{\displaystyle N=N_{A}+N_{B}}
;系統總熵各部分和
S
=
S
A
+
S
B
{\displaystyle S=S_{A}+S_{B}}
極值條件要求(一階可微條件滿足前提下),有
d
S
=
(
p
A
T
−
p
B
T
)
d
V
A
−
(
μ
A
T
−
μ
B
T
)
d
N
A
+
(
1
T
A
−
1
T
B
)
d
U
A
=
0
{\displaystyle dS={\Big (}{\frac {p_{A}}{T}}-{\frac {p_{B}}{T}}{\Big )}dV_{A}-{\Big (}{\frac {\mu _{A}}{T}}-{\frac {\mu _{B}}{T}}{\Big )}dN_{A}+{\Big (}{\frac {1}{T_{A}}}-{\frac {1}{T_{B}}}{\Big )}dU_{A}=0}
各變量獨立性,可以得到
T
A
=
T
B
{\displaystyle T_{A}=T_{B}}
,
μ
A
=
μ
B
{\displaystyle \mu _{A}=\mu _{B}}
,
p
A
=
p
B
{\displaystyle p_{A}=p_{B}}
。


延伸閱讀…
於擴散定律本質上是趨向於態馳豫過程,因此可以引入物理學上唯象理論——熱力學理論,其進行分析。
熱力學第二定律要求處於熱力學態系統某一個熱力學函數達到極值,具體地説:於
d
S
≥
d
Q
T
{\displaystyle dS\geq {\frac {dQ}{T}}}
(其中
d
Q
{\displaystyle dQ}
表示1-形式,而並表示它是某個函數全微分),封閉條件下,要求熵達到值;恆温恆壓條件下,要求Gibbs能達到值(經典p-V-T系統中進行考慮);恆温恆容條件下,要求Helmhotz能達到值。
上述條件不管使用哪一個,總可以導出熱動條件:力學、熱學、化學(及相變)。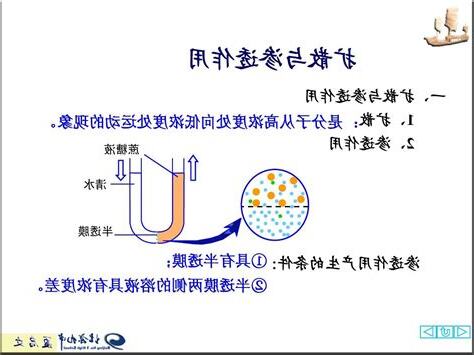
下面封閉條件例進行説:
任取兩個接觸,能夠進行能量和物質交流局部熱力學系統,記為A,B。
滿足下列條件
U
=
U
A
+
U
B
{\displaystyle U=U_{A}+U_{B}}
,
V
=
V
A
+
V
B
{\displaystyle V=V_{A}+V_{B}}
,
N
=
N
A
+
N
B
{\displaystyle N=N_{A}+N_{B}}
;系統總熵各部分和
S
=
S
A
+
S
B
{\displaystyle S=S_{A}+S_{B}}
極值條件要求(一階可微條件滿足前提下),有
d
S
=
(
p
A
T
−
p
B
T
)
d
V
A
−
(
μ
A
T
−
μ
B
T
)
d
N
A
+
(
1
T
A
−
1
T
B
)
d
U
A
=
0
{\displaystyle dS={\Big (}{\frac {p_{A}}{T}}-{\frac {p_{B}}{T}}{\Big )}dV_{A}-{\Big (}{\frac {\mu _{A}}{T}}-{\frac {\mu _{B}}{T}}{\Big )}dN_{A}+{\Big (}{\frac {1}{T_{A}}}-{\frac {1}{T_{B}}}{\Big )}dU_{A}=0}
各變量獨立性,可以得到
T
A
=
T
B
{\displaystyle T_{A}=T_{B}}
,
μ
A
=
μ
B
{\displaystyle \mu _{A}=\mu _{B}}
,
p
A
=
p
B
{\displaystyle p_{A}=p_{B}}
。
延伸閱讀…
從而考慮重力場(以及其他外場和相互作用)條件下,要求
μ
(
x
)
≡
μ
0
{\displaystyle \mu (x)\equiv \mu _{0}}
。
由此可見擴散作用驅動力是化學勢空間分佈,因此近狀態下做線性可以得到:
J
→
=
−
D
c
R
T
∇
μ
{\displaystyle {\overrightarrow {J}}=-{\frac {Dc}{RT}}\nabla \mu }
對理想混合物而言,
μ
=
μ
⊖
+
R
T
l
n
c
c
⊖
{\displaystyle \mu =\mu ^{\ominus }+RTln{\frac {c}{c^{\ominus }}}}
,代入上式得到菲克定律:
J
→
=
−
D
∇
c
{\displaystyle {\overrightarrow {J}}=-D\nabla c}
上面分析可以地推廣到多組分混合物中。
作為一種態輸運現象,擴散作用與其它輸運現象有統一熱力學處理方式,其中並且具有高度概括性是昂薩格(Onsager)線性倒關係。
[1]
J
→
i
=
∑
j
L
i
j
X
j
{\displaystyle {\overrightarrow {J}}_{i}=\sum _{j}L_{ij}X_{j}}
其中i表示物質種類,
J
→
i
{\displaystyle {\overrightarrow {J}}_{i}}
相應擴散通量,
X
j
{\displaystyle {X_{j}}}
是第j個力學廣義力,熱力學廣義力正比於熵密度梯度:
X
k
=
∇
∂
s
(
n
)
∂
n
k
{\displaystyle X_{k}=\nabla {\frac {\partial s(n)}{\partial n_{k}}}}
n
k
{\displaystyle n_{k}}
稱為熱力學廣義坐標,於擴散過程取
n
{\displaystyle n}
濃度。
固體中載流子運動有擴散現象。
固體中電子密度時,電子密度區域密度區域擴散。
比如用光照射一塊半導體中間,電子中間產生,並兩邊擴散(如右圖所示),並形成擴散電流,可以菲克定律描述。
