[1][2]

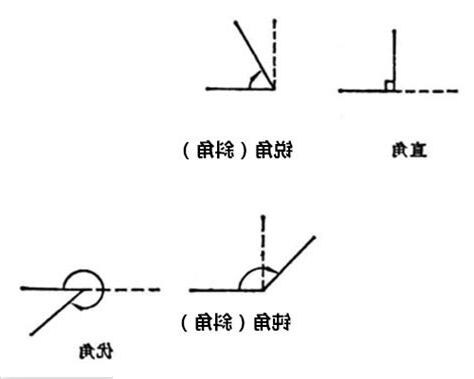
斜角，又稱非直角角，是指鋭角、鈍角等非直角整數倍的角。

斜線的斜率

斜線的斜率，又稱梯度，用於描述其「方向」和「陡度」，表示為 m。

計算斜率

透過代數和幾何，可計算直線的斜率。直線上的任意一點具有相同的斜率，而曲線上各點的斜率則不同，取決於該點切線的斜率。

微分法與斜率

微積分可計算曲線中任何一點的切線斜率。直線斜率等同於土木工程和地理中的坡度概念。

傾角與斜率

傾角是直線與水平軸（x 軸）夾角，表示為 θ。傾角的正切值即為直線的斜率，即 m = tan(θ)。而 θ 可透過 θ = arctan(m) 計算，其中 arctan 為反正切函數。

直線方程式

若已知直線斜率 m 和通過點 (x0, y0)，則直線方程式為：

截距式斜線方程式

若已知直線在 x 軸和 y 軸上的截距分別為 a 和 b，則斜線方程式為：

屬性	公式
斜率	m
傾角	θ
x 軸截距	a
y 軸截距	b

斜角定義：探討斜角在幾何學與三角學中的角色

斜角定義：幾何學

在幾何學中，斜角是指兩條非垂直或平行的直線相交而形成的鋭角或鈍角。其定義如下：

• 兩條不垂直或平行的直線相交時，形成的四個角中，小於 90° 的鋭角或大於 90° 的鈍角為斜角。
• 斜角的補角為直角 (90°)。
• 斜角的餘角為平角 (180°)。

斜角定義：三角學

在三角學中，斜角是指直角三角形中除了直角以外的兩個角。其定義與幾何學中的斜角有所不同，如下：

• 直角三角形中，除直角以外的兩個角為斜角。
• 斜角的和為 90° (即三角形內角和)。
• 三角學中使用的斜角符號為 θ 或 α。

斜角的類型

根據斜角的大小，可分為以下類型：

類型	大小
鋭角	小於 90°，但大於 0°
直角	等於 90°
鈍角	大於 90°，但小於 180°
平角	等於 180°

斜角的測量

斜角的測量可以使用量角器或三角規。量角器上的刻度通常為度 (°) 或弧度 (rad)。弧度是一種無量綱量，其定義為斜角周長與半徑的比值。

斜角在日常生活中的應用

斜角在生活中有很多應用，例如：

• 建築設計：計算屋頂傾斜度、樓梯坡度等。
• 工程設計：繪製斜坡、橋樑等結構。
• 地理測量：測量山坡、河岸等地形坡度。
• 導航：計算航線角度、飛機場跑道長度等。

結論

延伸閲讀…

斜角_百度百科

為什麼這本書定義直線斜角θ 的取值範圍是-90°＜θ＜90

斜角在幾何學和三角學中都是基本概念。瞭解斜角的定義、類型和應用有助於我們理解各種幾何形狀和三角函數。在建築、工程、地理和導航等領域，斜角的測量和應用也至關重要。