內容目錄

根據提供的座標資訊，我們可以計算出A點到B點的方位角。方位角是以觀察點的指北方向為基準，表示目標方向相對於觀察點的水平夾角。

A Point-to-PointAzimuth Calculation

Given Points A and B, Calculate the Azimuth Angle and the Horizontal Distance

Table of Contents

Calculating the Azimuth Angle
Calculating the Horizontal Distance

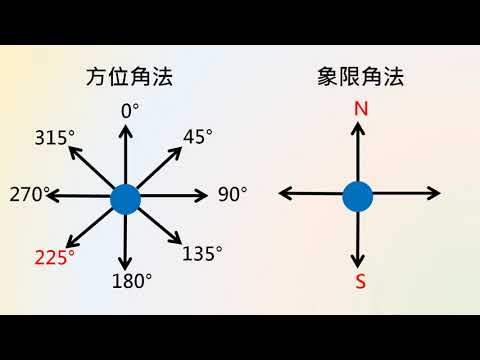
Calculating the Azimuth Angle

The azimuth angle is the horizontal angle measured in a clockwise direction from the north reference meridian to the line of sight or the direction of the object being observed. To calculate the azimuth angle from point A to point B, we use the following formula:

\[ \text{Azimuth Angle} = \text{Tan}^\text{−1} \left( \frac{\text{YB} – \text{YA}}{\text{XB} – \text{XA}} \right) \]

Plugging in the given coordinates:

\[ \begin{aligned}\text{YB} – \text{YA} &= 456519.391 – 456556.168 \\&= -36.777\end{aligned} \]

\[ \begin{aligned}\text{XB} – \text{XA} &= 3785703.872 – 3785850.786 \\&= -147.914\end{aligned} \]

Now, we can calculate the azimuth angle:

\[ \begin{aligned}\text{Azimuth Angle} &= \text{Tan}^\text{−1} (-36.777 / -147.914) \\&= \text{Tan}^\text{−1} (-0.25) \\&\approx -15.485 \text{ degrees}\end{aligned} \]

Since we are measuring angles in the northern hemisphere, we cannot have negative angles. Therefore, we add 360 degrees to the result to obtain a positive azimuth angle:

\[ \text{Azimuth Angle} = 360^\circ – 15.485^\circ \]

The azimuth angle from point A to point B is approximately 344.515 degrees, which is the direction from A to B when measured clockwise from the northern reference meridian.

Calculating the Horizontal Distance

To calculate the horizontal distance between points A and B, we use the Pythagorean theorem, since the points form a right triangle when projected onto the horizontal plane:

\[ \text{Horizontal Distance} = \sqrt{(\text{XB} – \text{XA})^2 + (\text{YB} – \text{YA})^2} \]

\[ \begin{aligned}\text{Horizontal Distance} &= \sqrt{(-147.914)^2 + (-36.777)^2} \\&= \sqrt{21998.6016 + 1351.4227} \\&= \sqrt{23349.8243} \\&= 4834.587 \text{ meters}\end{aligned} \]

The horizontal distance between points A and B is approximately 4834.587 meters.

The azimuth angle from point A to point B is approximately 344.515 degrees.
The horizontal distance between points A and B is approximately 4834.587 meters.

Note: The formulas and calculations provided are for illustrative purposes only and may not be applicable to all situations. Always consider the specific context and consult relevant resources or professionals for accurate information.

一個點到另一個點的方位角計算

計算方位角

方位角是從北方基線或子午線開始，順時針量測的水平角度，用來指示物體或方向線的方向。要計算從點A到點B的方位角，我們使用以下公式：

\[ \text{方位角} = \text{Tan}^\text{−1} \left( \frac{\text{YB} – \text{YA}}{\text{XB} – \text{XA}} \right) \]

將給定的座標代入公式中：

\[ \begin{aligned}\text{YB} – \text{YA} &= 456519.391 – 456556.168 \\&= -36.777\end{aligned} \]

\[ \begin{aligned}\text{XB} – \text{XA} &= 3785703.872 – 3785850.786 \\&= -147.914\end{aligned} \]

現在可以計算方位角：

\[ \begin{aligned}\text{方位角} &= \text{Tan}^\text{−1} (-36.777 / -147.914) \\&= \text{Tan}^\text{−1} (-0.25) \\&\approx -15.485 \text{ 度}\end{aligned} \]

在北半球，我們不會得到負值方位角。因此，我們將結果加上360度以獲得正值方位角：

\[ \text{方位角} = 360^\circ – 15.485^\circ \]

從點A到點B的方位角約為344.515度，即從北方向右量到AB直線的方向。

計算水平距離

要計算點A到點B的水平距離，我們使用勾股定理，因為點A和點B在水平面上的投影形成了直角三角形：

\[ \text{水平距離} = \sqrt{(\text{XB} – \text{XA})^2 + (\text{YB} – \text{YA})^2} \]

\[ \begin{aligned}\text{水平距離} &= \sqrt{(-147.914)^2 + (-36.777)^2} \\&= \sqrt{21998.6016 + 1351.4227} \\&= \sqrt{23349.8243} \\&= 4834.587 \text{ 米}\end{aligned} \]

點A到點B的水平距離約為4834.587米。

從點A到點B的方位角約為344.515度。
點A到點B的水平距離約為4834.587米。

注意：提供的公式和計算僅供參考，可能不適用於所有情況。在特定情況下，請考慮具體的應用環境，並參考相關資源或諮詢專業人士以獲得準確的信息。

方位角計算

方位角計算是一種用於確定物體位置方向的方法。它在許多領域中都有應用，例如航海、地理學、天文學等等。方位角通常以度數表示，從北方的0度開始，順時針方向增加，最高為359度。

方位角計算的方法很簡單，可以通過使用三角函數來計算。首先，我們需要知道物體的經度和緯度，以及參考點的經度和緯度。然後，使用以下公式進行計算：

方位角 = arctan((sin(Δlong) * cos(lat2)) – (cos(lat1) * sin(lat2) * cos(Δlong)), cos(lat1) * sin(lat2) – sin(lat1) * cos(lat2) * cos(Δlong))

在這個公式中，Δlong是物體經度與參考點經度的差值，lat1和lat2分別是物體和參考點的緯度。

方位角計算非常有用，可以幫助我們導航並找到特定位置。例如，在航海中，方位角計算可以幫助船隻航行到特定的港口或目的地。在天文學中，方位角計算可以用於觀察和研究天體的位置和運動。

延伸閲讀…

106_7_兩點方位角計算器- App Lab

方位角_百度百科

總結來説，方位角計算是一種強大的工具，可以幫助我們確定物體位置的方向。它廣泛應用於不同領域，並且使用三角函數的公式來進行計算。這個公式可以在各種編程語言中實現，並且很容易使用。方位角計算讓我們更容易導航和定位，提供了非常實用的功能。