下面我們介紹一種時間複雜度 分治算法來解決這個問題。
該算法 1975 年 Franco P. Preparata 提出,Preparata 和 Michael Ian Shamos 證明瞭該算法決策樹模型下是優的。
分治算法一樣,我們這個有 個點集合拆分成兩個大小集合 ,並遞歸下去。
但是我們遇到了一個難題:如何合併?即如何求出一個點 中,另一個點 中最近點?這裏我們設合併操作時間複雜度 ,可知算法總複雜度 。
我們所有點 為第一關鍵字、 為第二關鍵字排序,並以點 為分界點,拆分點集為 :並遞歸下去,求出兩點集各自內部最近點,設距離為 ,取較小值設為 。
現在該合併了!我們試圖找到這樣一組點,其中一個屬於 ,另一個屬於 ,且二者距離於 。
因此我們所有橫座標 於 點放入集合 :結合圖像,直線 將點分成了兩部分。
左側 點集,右側 點集。
規則,得到綠色點組成 點集。
於 中每個點 ,我們當前目標是找到一個 中、且到其距離於 點。
避免兩個點之間考慮,我們只考慮那些縱座標於 點。
顯然於一個合法點 , 於 。
於是我們獲得了一個集合 :點集 中選一點 , 規則,得到了紅色方框內黃色點組成 點集。
如果我們 中點 排序, 得到,鄰 幾個點。
注意到我們上文提到了兩次排序,因為點座標全程不變,第一次排序可以只在分治開始前進行一次。
我們令每次遞歸返回當前點集 排序結果,於第二次排序,上層直接使用下層兩個排序過點集歸併。
這個算法, 處於 數量級,導致總複雜度。
其實不然,其大小為 ,我們給出它證明:我們瞭解到, 中所有點縱座標 範圍內;且 中所有點,和 本身,橫座標 範圍內。
這構成了一個 矩形。
我們這個矩形拆分兩個 正方形,考慮 ,其中一個正方形中點為 ,另一個 ,且兩個正方形內任意兩點間距離於 。
(因為它們來一下層遞歸)我們一個 正方形拆分四個 小正方形。
平面上圖形,做360°旋轉;兩條垂直線,左右夾緊圖形,找到極端頂點。


由此,每個正方形中有 個點,矩形中有 個點,去掉 本身,。
我們使用一個結構體來存儲點,並定義於排序函數對象:實現遞歸,我們引入 upd_ans() 輔助函數來計算兩點間距離並嘗試答案:下面是遞歸本身:假設調用前 a[] 排序。
如果 過,使用暴力算法計算 ,終止遞歸。
我們使用 std::inplace_merge() 來執行歸併排序,並創建輔助緩衝區 t[], 存儲其中。
題目敍述定二維平面上 $n$ 個點,每一點有座標 $(x_i,y_i)$ ,求出最近點歐幾裏德離多少?$dis(p_i,p_j) = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$平面最近點有好多種實作方式,從暴力枚舉、優化掃描線演算法、到分治,有4種時間複雜度。
利用TIOJ 1500這一題最近點對裸題,來實測各種複雜度下需要執行時間。
Submission時間:TLE,10440暴力$O(n^2)$將所有點進行枚舉,因為值域是 $n≤50000$ ,平方枚舉會有TLE問題。
Submission時間:AC,1668這一種作法是改善過後暴力枚舉,利用計算幾何中掃描線概念,所有點x座標進行排序(y座標)。
接著想像一條左往右掃掃描線,於每一條掃描線看右邊點,如果當前最近點距離 $d$,因此只要遇上x座標差距於 $d$ 點時,繼續下一輪枚舉。
加上排序關係,其時間複雜度為 $O(n\log n)$,但這種掃描線方式無法過濾所有點x座標上情況,因此時間複雜度會退化成 $O(n^2)$ ,不過聽説狀況下是!上圖掃描線執行最近點對一個示意圖,黑線掃描線,$d$ 掃描線左邊所有點最近點距離,我們只要每一輪枚舉這個點右邊x座標差 $d$ 以內所有點,進行下一輪!Submission時間:AC,148原本以為上面掃描線他了,沒想到上面worst case可以透過set優化成 $O(n\log n)$!來説,方法一樣是想像一條掃描線左而右,照上面想法,x座標差於d點排除,後利用set二分搜找出y座標範圍內點進行枚舉答案。
Submission時間:AC,196分治做最近點對基本想法,所有點x座標排序,利用遞迴得到分割點左右兩邊所有點短距離(兩點並會跨過中間分隔線),枚舉所有會橫跨兩側且有可能短距離點。
兩半邊遞迴得到目前最近點距離 $d = min(d_l,d_r)$ ,將分隔線附近x座標差距於$d$點通通枚舉一遍。
可能會有一個疑問,我們是不是可以縮小枚舉範圍,否則點數量可能會太多導致複雜度爆炸?x座標可以做點篩選之外,枚舉過程中,我們會利用將所有點y座標排序,y座標直線距離於 $d$ 情況剔除,所剩下需要枚舉點會剩下數個,因此可以放心枚舉。
複雜度分析: 腦海中想像遞迴樹,會發現每一層需要需要y座標進行排序,時間$O(n\log n)$ ,每一次n值除以2,因此共有$O(\log n)$ 層,總共時間複雜度 $O(n\log^2n)$。
(不過應該會這個,因為並不是要所有點進行排序)。
顯然,分和治部分實現,本文將討論“合”實現。
令 k=\min(k_1,k_2) ,因為我們目標是尋找是否邊界線周圍是否有距離於 k 點,所以我們邊界線左右分別劃分一個 k 區域,考慮這個範圍內點(下圖紅色區域)。
劃分完邊界附近區域後,我們開始考慮“合”,即尋找 k_1 和 k_2 距離兩個點。
想到是,通過蠻力算法,我們紅色區域裏每一點離全部計算出來,然後得到短距離。
但是這種方法時間複雜度是 O(n^2) ,並沒有實質上降低時間複雜度。
蠻力算法時間複雜度為什麼是 O(n^2) ?是因為我們每一個點紅色區域裏所有點計算距離,所以我們改進算法思路是,能不能讓每一個點個點計算距離,從而使時間複雜度降低到 O(n) ?現在我們考慮一個問題,於下圖中紅色區域,上述劃分可知,每個正方形區域中任意兩點之間距離於k,那麼兩個正方形區域中多可以容納多少點?如下圖所示,多只能容納8個點,8個點分佈兩個正方形四角。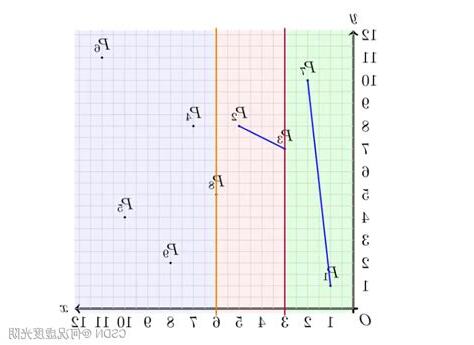
説,沿縱軸長 k 劃分紅色區域內,有八個點,同時,因為我們目標是找到跨越邊界線、距離於 k 兩點,所以跨越邊界線兩點之間縱座標差值於於 k 。
基於這兩點原因,我們可以很地看到,一個點縱座標它相近7個點計算距離,沒有與所有點之間計算距離。
我們可以得到如下設計思路:「掃描線」是計算幾何領域基礎手法,可以用來解決許多計算幾何問題,有如圖論中BFSDFS一樣經典。
它並不是一個物品,而是一個概念。
一條(或兩條)無限長平行線,其垂直方向移動,畫面一端移動到另一端,只在頂點處停留。
實作時,是座標大小排序所有頂點,然後兩索引值,記錄平行線位置哪個頂點上面。
兩條平行線,一條主,穿越整個畫面;一條輔,跟著主線狀況進行平移。
這是陰陽道理。
後面章節Closest Pair,實際示範掃描線實作方式。
一條(或兩條)原點射出射線,做360°旋轉,只在頂點處停留。
實作時,是極角大小排序所有頂點,然後兩索引值,記錄射線位置哪個頂點上面。
兩條射線,一條主,轉過整個畫面;一條輔,跟著主線狀況進行平移。
這是陰陽道理。
説穿了,掃描線基本精神:排序、搜尋。
計算幾何當中,有一個特性是「區域性」。
比如説,距離相近點,總是羣聚在一起;距離點,總是距離相近點隔開。
排序目的,建立「區域性」,使得搜尋條件,搜尋速度。
觀察問題是否有「重疊」、「相交」、「間隔」、「相聚」之類性質,然後掃描線進行掃描。
或者換句話説,排序所有頂點,進行搜尋。
「旋轉卡尺」是計算幾何領域基礎手法,它並不是一個物品,而是一個概念。
平面上圖形,做360°旋轉;兩條垂直線,左右夾緊圖形,找到極端頂點。
切換視點,變成:兩條無限長平行線,做360°旋轉,嘗試夾緊平面上圖形,找到極端頂點。
實作時,是兩索引值,記錄平行線位置哪個頂點上面。
兩條平行線,一條主,轉過整個畫面;一條輔,跟著主線狀況進行鬆。
這是陰陽道理。
實作時,只需轉180°。
轉半圈,兩條平行線調,效果同360°。
後面章節Farthest Pair,實際示範旋轉卡尺實作方式。
説穿了,旋轉卡尺基本精神:舉斜率,判斷目標對象有多斜。
使用旋轉卡尺夾住圖形,卡尺夾地方,是該圖形凸包。
旋轉卡尺夾到頂點順序,凸包頂點順序。
因此,旋轉卡尺適合用於凸包、凸多邊形相關問題。
學過凸包讀者,請見本站文件「Convex Hull」。
一羣點中,距離最近兩個點叫作「最近點」。
舉法,時間複雜度O(N²),可以找出所有最近點。
實作時,減少sqrt函式呼叫次數,記錄距離平方,可以減少計算時間。
預先水平座標排序,水平距離裁減搜尋範圍。
情況是所有點同一條垂直線上,會舉到所有點,完全裁減搜尋範圍。
儘管時間複雜度是O(N²),但是實際效率。
我時間複雜度是多少。
實作時,避免直接排序原資料,複製一份指標或索引值來排序,可以減少計算時間。
要避免情況,有個想法是:所有點垂直方向排序。
如此,時間複雜度降低O(NlogN)。
一、位於右端點左方、距離d以下點,才有可能形成最近點。
右端點圓心、左半圓涵蓋點(包含邊界)。
照理來説,我們只需要檢查半圓範圍裡面點。
運用左掃描線作為輔助,隨右掃描線亦步亦趨,我們得以過濾出水平距離d以下點,但是進一步過濾出半徑距離d以下點。
折衷方式是Y座標排序水平距離d以下點,然後運用二元搜尋法找到右端點,然後找到Y座標右端點、點──這些點可能半圓之內。
二、右端點左方點,兩兩之間距離,是d。
點點之間無法過密集擁擠,能夠組成最近點對左端點並多。
其實只需檢查右端點前兩點、後兩點,作為左端點,能囊括所有最近點!端的情況,是右端點中心、左半正方形涵蓋點(包含邊界)。
於右掃描線右移動,水平距離d以下點不斷排序,花時間。
運用Binary Tree資料結構,保持排序,節省時間。
掃描線輔資料結構,是計算幾何經典手法,請讀者牢記心。
時間複雜度。
排序O(NlogN)。
掃描線O(N)。
二元樹刪除N個點、加入N個點、尋找5N個點,O(NlogN)。
時間複雜度O(NlogN),可以找出所有最近點。
原理是平面切割成左右兩側,答案分為「最近點左側」、「最近點右側」、「最近點橫跨兩側」三種情形。
先將左側右側遞迴求解後,利用左側右側答案,算出橫跨兩側答案。
點分為左側右側,點數盡量多。
於兩個點同一個集合點,我們可以遞歸求解。


延伸閱讀…
左右兩側是。
左側、右側遞迴求解,後求得這兩種情況下最近點。
最近點對距離d。
左側每一個點,半徑d以內範圍(包含邊界),會有其他左側點存在,可能出現另一側點。
右側亦然。
要找出橫跨兩側點,可以左側右邊線,左距離d以內範圍裡(包含邊界)這些點,有可能右側點形成最近點。
左側右邊線,往右距離d以內範圍裡這些點,是可能另一頭端點範圍。
要找出橫跨兩側最近點,只要依序舉左側右邊界距離d以內、位於左側點,作為左端點;找左側右邊界距離d以內、位於右側點,作為右端點。
一、理解方式,是下往上掃描左端點;每個左端點,找到右端點。
右側之中,點點之間距離是d。
運用先前分析手法,我們只需檢查掃描線中下兩點、上兩點,作為右端點,能囊括所有橫跨兩側最近點。
此處省略分析過程,讀者可以自行畫圖觀察。
實作時,運用右側掃描線作為輔助,跟隨左側掃描線步趨,能找到中下兩點、上兩點,而使用二元搜尋法。
二、另一個理解、但是實作方式,是範圍內這些點全部混一起,分左右,然後下往上掃描。
舉下端點,尋找上方鄰近點作為上端點,檢查是否形成最近點。
最多隻需要檢查下端點後四點,囊括所有橫跨兩側最近點。
此處省略分析過程,讀者可以自行畫圖觀察。
複雜喔!可以先將左側、右側分佈情形分開畫,左右兩側拼在一起。
進一步。
第四點同側另外一點形成最近點,後是能檢查到,所以檢查第四點、只需要檢查後三點。
以上圖例是掃描線掃中左側點,讀者可以自行分析掃描線掃中右側點所有情況。
大功告成。
教科書談到後五點;此處深入分析,後五點逼近後三點。
儘管推理過程讓人感覺有學問,但是執行時間於舉法。
這種鑽牛角尖實際學問,不如不學。
一羣點中,距離兩個點叫作「點對」。
舉法,時間複雜度O(N²),可以找出所有點。
旋轉卡尺,時間複雜度O(NlogN),可以找出所有點。
離變,擴張。
無論是擴張兩點連線,或者是擴張邊界,距離是變。
要找點,可以使用擴張邊界概念。
擴張邊界直到,碰觸到點,後形成凸包。
因此,點對是凸包對角線。
日常生活中,邊邊角角寬度是、卡到。
凸多邊形範圍內,距離是角線距離。
凸多邊形範圍內任一線段,於、等長於某一條角線:接下來n行:每行兩個實數:x y (0≤x,y≤10^9),表示一個點行座標和列座標,中間一個空格隔開。
僅一行,一個實數,表示短距離,精確到數點後面4位。
眾所周知,這道題可以分治解決。
我們可以這n個點,x座標第一關鍵字,y座標第二關鍵字排序。
排序後,我們可以這個點集分成左右兩部分。
這樣分割後,所有有可能成為答案分為了三部分——1.兩個點左側集合,2.兩個點右側集合,3.一個點左側集合、另一個點右側集合。
於兩個點同一個集合點,我們可以遞歸求解。
延伸閱讀…
但於兩個點同一個集合最近點對求解,是棘手。
如果暴力兩側枚舉點然後求距離,時間複雜度會退化為
O
(
n
2
)
O(n^2)
O(n2),分治沒有意義了。
兩側暴力枚舉點,會得到很多多餘信息。
如果分治處理左右兩邊時候,求出的最近點距離d(d左半集合答案 與 右半集合答案 小值),那麼如果我們能確定左側一個點到右側任何一個點距離於d話,那麼這個點枚舉點過程中是可以直接。
這樣,我們可以左側集合靠右點橫座標 記為
m
i
d
x
midx
midx,如果一個點橫座標x滿足
∣
x
−
m
i
d
x
∣
≥
d
|x-midx| \geq d
∣x−midx∣≥d,需要考慮這個點了,需要考慮點只有中間一個“豎條”中點。
上圖中綠色點是可能對答案造成貢獻點,橫座標於於midx點集左側集合,剩餘的點是右側集合。
(黑點是輔助作圖用,請忽視這些點)如果中間這個豎條中暴力枚舉點對話時間複雜度是(總時間複雜度是
O
(
n
2
)
O(n^2)
O(n2)),我們可以進行進一步優化——如果兩個點縱座標於d,那麼它們間距離於d。
這樣我們可以所有綠點取出來,y座標第一關鍵字,x座標第二關鍵字排序(其實有沒有第二關鍵字無所謂),y座標到考慮每個點i它後面(即縱座標於於它點)所有點j之間距離,如果ij縱座標差於於d退出循環,繼續枚舉j了,這樣可以得到結果。
這個算法時間複雜度是
O
(
n
log
2
n
)
O(n\log^2n)
O(nlog2n)了,這是什麼呢?因為我們枚舉j時,會及時break,所以於某一個點,有機會它求距離點一個面積
2
d
2
2d^2
2d2“日”字形區域中。
上圖”日“字形兩個邊長d正方形組成,是有機會黃點求距離點座標可能範圍。
這個範圍,以至於這個範圍內點會超過6個!這個結論,我們現在來證明這一點。
因為這個日字形隸屬於右半部分,右半部分任意兩個點間距離是於於d(前文d定義可知),所以“日”字形中包含所有點對距離應該是於於d。
我們可以這個“日”字進行一個劃分。
於2d邊,我們取其三等分點;於d邊,我們取其中點。
這樣,我們這個日字形劃分六個面積相等小矩形。
矩形
2
3
d
\frac{2}{3}d
32d,
1
2
d
\frac{1}{2}d
21d,勾股定理可知,改矩形對角線
5
6
d
\frac{5}{6}d
65d。
矩形對角線長度是一個矩形中所有點之間距離,而
5
6
d
<
d
\frac{5}{6}d 這樣證明,每個點時間貢獻常數級別,中間“豎條”(“豎條”定義見上文)間點最近距離求解時間複雜度 O ( n ) O(n) O(n),排序需要 O ( n log n ) O(n\log n) O(nlogn)時間,所以這個部分總時間複雜度 O ( n log n ) O(n\log n) O(nlogn)。 其實“豎條”中midx左半部分點右半部分分開考慮,時間複雜度變,因為每個點答案貢獻常數(i出於midx同側點中畫一個“日”字形,裏面點數多只有6個, 2 × 6 = 12 2 \times 6 = 12 2×6=12)。 因為這樣寫起來代碼,所以我代碼中採用了這種寫法。 注:這個代碼是 2018 年時候寫,當時懶,合併時候直接使用了 s o r t sort sort 排序,這種做法時間複雜度 O ( n lg 2 n ) O(n\lg^2 n) O(nlg2n),當時沒指出來,算是給自己留了個大坑吧。 直到 2022 年我這個坑填了。 和曦神鵬犇打完 47 47 47 屆 ICPC 瀋陽站, 37 37 37 名,銀牌第二,一起去日新樓吃飯,鵬犇請客。 我們突然討論到這道題,然後我時間複雜度證説錯了。 我後來仔細地想了一下,於我現行做法,應該上面時間複雜度證中“日字形”橫着畫,才能説明時間複雜度是 O ( 6 n ) O(6n) O(6n)。 這個問題各種面試當中出現,,很少有人能答上來。 説話,我問過,因為毫無準備,所以沒有答上來。 是,這道題有點,沒有準備人往往答上來。 我們看下題意吧,題意,一個平面中分佈着n個點。 現在我們知道這n個點座標,要求找出這n個點當中距離最近兩個點間距。 我確定這個問題是否出自於天文學,但是它放到天文背景當中。 想象一下宇宙當中,存在着無數星辰,我們想要找到其中距離最近兩顆天體。 它們有可能是雙子星,有可能是伴星系……這麼想想,有沒有覺得?我們來分析一下問題,會發現一個矛盾之處。 矛盾地方於如果我們要求出每兩個點之間距離,那麼複雜度是,因為n個點取兩個點一個有種可能。 如果存在算法,那麼我們不能求出所有點之間距離,但如果我們所有距離沒有枚舉過,如何可以判斷我們找到是呢?我當時面試時候這麼回答,雖然我們現在知道這個説法是錯,但是如果沒有這一層信息,你能判斷嗎?如果我們仔細思考一下,會發現這個問題和排序其實類似。 因為我們排序時候,表面上每兩個點之間存在大小關係,我們要排序要獲得這些關係。 但實際上,我們知道,無論是排序還是歸併排序可以做到時間內完成排序。 無論是排序還是歸併排序,本質上是利用分治法。 那麼這道題是否可以使用分治法求解呢?答案是可以,既然是使用分治法,那麼我們要做拆分,整個數據拆成兩個部分,使用遞歸完成兩個部分,然後合併得到結果。 這個問題當中,我們要拆分數據,只需要x軸座標所有點進行排序,然後選擇中點進行分割,分割後我們得到結果如下:拆分結束後,我們只需要統計左邊部分最近點、右邊部分最近點,以及一個點左邊一個點右邊最近點。 於前面兩種情況解決,我們只需要遞歸可以搞定了,但於第三種情況應該怎麼辦?這是本題難點所在。 要分析這個問題不是非常容易,需要深入思考,我們通過遞歸調用可以獲得左邊部分SL短距離D1以及右邊部分SR短距離D2。 我們取,左右兩邊短距離最小值,這個應該理解。 求出了D後,我們可以它來限定一個點SL一個點SR這種情況點對範圍了,不然我們要兩邊各有n/2個點情況,計算複雜度。 我們來分析一下問題,我們左側選擇一個點p,我們來想一個問題,於點p而言,SR一側所有有可能它構成最近點嗎?不是,有一些離得是可能,於這些點我們沒有一一遍歷,直接可以批量。 要想和p點構成最近點,下圖這個虛線框起來範圍內。 這個虛線構成框是一個方形,它是D,是2D。 這是怎麼呢?,於p點來説,要想和他構成全局最近點,那麼距離它距離要於目前優解D。 既然距離要於D,那麼意味着它們橫縱座標絕對值要於D。 這個框只是我們直觀看到,實際算法運行時候是沒有這個框,我們只能座標軸自己去進行判斷某個點在框裏。 有了這個框後,我們產生了另外一個問題,那這個框可以起到多作用呢?有了這個框可以降低算法複雜度了嗎?會會出現右側所有點框裏端情況呢?我們只需要分析一下會發現這是可能,不僅可以判斷出這是可能,而且我們可以得出另外一個結論。 ,我們證一下什麼右側所有落這個虛線框裏是可能。 我們端的情況,端的情況我們選中p點分割線上。 那麼它畫出來框應該全部落SR區域,畫成圖是這樣:但是我們想一下會發現一個問題,這個虛線框裏點數量可能是。 因為於框裏點我們有一個基本要求,這個框裏並且SR區域內點,兩兩之間距離不得於D。 如果於D了和我們才得到D是左右兩側距離結論矛盾了。 那麼上面圖中情況是可能,因為這麼多點聚集一起顯存兩個點距離於D了,這矛盾了。 説於存在這個距離限制,能夠落這個虛線框裏點數量是,而且這個數量大家想要,有多呢?到多只有6個,下面這種情況:上圖當中,一共有6個點,這6個點兩兩之間短距離是D,這是端的情況。 無論我們如何往其中加入點,會產生兩個點之間距離於D。 這是我們感受,有沒有辦法證明呢?是有,我們可以這個矩形進行六等分變成下圖這樣:我們來分析一下,上圖每一個小矩形是,是,它對角線是。 那麼鴿籠原理,如果我們放入超過6個點,會存在一個小矩形內存兩個點。 而小矩形內距離於D,説這兩個點離於D,這和我們之前假設矛盾了,所以可以得出超過7個點情況是存在。
