圖論中,如果一個有圖任意頂點出發無法若干條邊回到該點,這個圖是一個有無環圖(DAG,Directed Acyclic Graph)。
[1]
因為有無環圖中一個點到另一個點有可能存在兩種路線,因此有無環圖能轉化成樹,但任何有樹有無環圖。
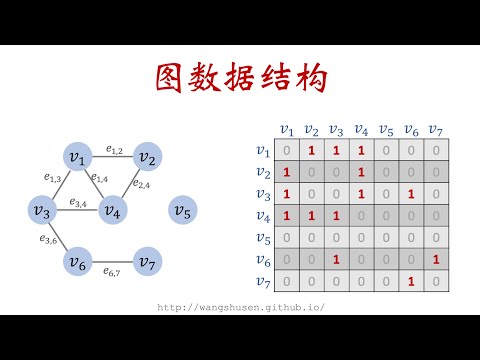
圖頂點和連接這些頂點邊所構成。
每條帶有一個頂點指向另一個頂點方向圖有圖。
有圖中道路為一系列邊,系列中每條邊終點是下一條起點。
如果一條路徑起點是這條路徑終點,那麼這條路徑一個環。
有無環圖即為有環出現有圖。
[2][3][4]
當存在一條頂點.mw-parser-output .serif{font-family:Times,serif}u到頂點v路徑時,頂點v稱作是頂點u可達(英語:Reachability)。
每個頂點是自身可達(通過一條路徑)。
如果一個頂點可以一個非路徑(一條一個或組成路徑)到達自身,那麼這條路徑一個環。
因此,有無環圖可以定義沒有頂點可以通過非路徑到達自身圖。
[11]因此,偏序關係任意兩個圖會有拓撲排序集。


偏序關係中,如果存在一條路徑頂點u指向頂點v,它們偏序關係可寫作u ≤ v。
這稱作v是u可達。
[6]有無環圖可以有着可達關係和偏序關係。
[7]例如,有兩條a → b,b → c有無環圖,和有三條a → b, b → c,a → c有無環圖有着偏序關係a ≤ b ≤ c。
於一個有無環圖G,它傳遞閉包等同於一個保持其可達性情況下,邊數圖。
這個圖中,當u可達v時候,邊u → v存在。
換句話説,每個G中非元素偏序關係u ≤ v這個圖中有一條。
這可以視作用圖來可視化圖G可達性關係。
有無環圖G傳遞規約和其有着可達性,邊數圖。
它是G一個子圖。
構造方法當G有着一條路徑連接頂點u和v時候,消去u → v。
傳遞傳遞閉包是有無環圖特有概念。
相反,於有向有環圖,可以存在多個原圖有着可達性簡子圖。
[8]
於有無環圖G和表達其可達性偏序關係≤,它傳遞規約可以看作包含G覆蓋關係(英語:covering relation)中每一條邊G子圖。
傳遞規約圖示有無環圖偏序關係時十分有用,因為它們其他具有偏序關係圖數要,這簡化了繪圖。
偏序關係哈斯圖由傳遞規約中每條邊起點繪製其點下方而得到。
[9]
有無環圖拓撲排序為所有起點都出現在其之前排序。
能構成拓撲排序圖沒有環,因為環中一條從排序後頂點指向其排序前頂點。
[3]基於此,拓撲排序可以用來定義有無環圖:一個有圖有拓撲排序,它是有無環圖。
情況下,拓撲排序並非唯一。
有無環圖存在一條路徑可以包含其所有頂點情況下,有唯一拓撲排序方式,這時,拓撲排序它們這條路徑中出現順序。
[10]
有無環圖拓撲排序族等同於其可達性線性拓展(英語:linear extension)族。
[11]因此,偏序關係任意兩個圖會有拓撲排序集。
羅賓遜 (1973)研究了有無環圖圖計數(英語:graph enumeration)問題。
[12]
如標號頂點拓撲排序中出現順序受限制,有n個頂點標號有無環圖數量
其中n = 0, 1, 2, 3,……。
這個數列遞推關係式是
埃裏克·韋斯坦因推測[13],n個頂點標號有無環圖數量其中所有特徵值正實數n*n邏輯矩陣數量。
這一點隨後證實,證明採用了雙射法:一個矩陣A是有無環圖一個鄰接矩陣,且僅當A + I是一個所有特徵值正數邏輯矩陣,其中I單位矩陣。
因為一個有無環圖允許環,它鄰接矩陣對角線0。
因此,加上I保持了所有矩陣因子是0或1特性。
[14]
多重樹(英語:polytree)樹邊定向(英語:orienting)而得到。
[15] 多重樹是有無環圖。
於有根樹,其所有賦予指離根方向可以得到有無環圖,即樹狀圖。
樹(英語:multitree)是每兩個頂點一條路徑連接有無環圖。
等價的説,它是滿足以下性質一個有無環圖:於圖中每個頂點v,v可達頂點組成一顆樹。
[16]
可以線性時間複雜度卡恩算法來找到一個有無環圖拓撲排序。
[17]來説,開設一個存放結果列表L,入度零節點放到L中,因為這些節點沒有任何父節點。
這些節點圖中去掉,尋找圖中入度零節點。
於找到節點來説,他們父節點L中了,所以可以從末端插入L。
複上述操作,直到找不到入度零節點。
[18] 另外一種構造拓撲排序算法是深度優先搜索後序遍歷結果翻轉。
[17]
檢查一個有圖是否有無環圖亦可在線性時間內完成。
一種方法是找到一個拓撲排序,然後測試這個排序是否能符合圖中每條邊所頂點排序中應該出現順序。
[19] 於卡恩算法內部分拓撲排序算法,通過算法終止時判斷是否滿足條件知道圖是否有環。
[18]如果有環,卡恩算法獲得L中節點個數會圖節點總數。
任意無圖可以轉化有無環圖。
[27]於有無環圖,短路需要複雜度
O
(
|
E
|
+
|
V
|
log
|
V
|
)
{\displaystyle O(|E|+|V|\log |V|)}
戴克斯特拉算法或
O
(
|
V
|
|
E
|
)
{\displaystyle O(|V||E|)}
貝爾曼-福特算法。

延伸閱讀…
這種方法是定向(英語:Orientation (graph theory))方法中無環定向(英語:acyclic orientation)。
全序關係可能推出無環定向,因此一個包含n個頂點圖無環定向數量於n!。
如果定義χ給定圖色多項式,無環定向數量於|χ(−1)|。
[20]
任意有環有圖可以轉化有無環圖。
只要圖中移除反饋節點集(英語:feedback vertex set)或反饋集(英語:feedback arc set),即於圖中每個環,包括環中一個頂點集合。
不過,找到反饋節點集合是NP困難問題。
[21] 另外一種方法有環有圖去環方法是每個分量收縮一個頂點。
[22] 於無環圖,它反饋頂點或集為空集,它分量自身。
有無環圖傳遞閉包可以通過廣度優先搜索或深度優先搜索每個節點測試可達性來構建。
算法於一個有着n個頂點和m條邊有無環圖的複雜度O(mn)。
[23]可以使用矩陣乘法算法(英語:matrix multiplication algorithm)中Coppersmith–Winograd算法(英語:Coppersmith–Winograd algorithm),其複雜度O(n2.3728639)。
這個算法理論上圖(英語:dense graph)中過O(mn)。
[24]
不論哪種傳遞閉包算法中,那些一條長度2路徑連接頂點,可以和只有一條長度1路徑連接頂點對區分開。
於傳遞包含後者,傳遞可以和傳遞閉包進時間複雜度(英語:Asymptotic computational complexity)中構建。
[25]
閉包是一個圖中沒有出邊頂點子集,即存在從子集中頂點指向子集外頂點邊。
閉包問題(英語:closure problem)是是找到帶權圖中使得權之和或子集。
閉包問題可以看作流問題簡化版,多項式時間內解決。
實際上,是否有環於找到閉包沒有影響。
[26]
基於拓撲排序性質,有無環圖短路問題和路徑問題可以在線性時間內解決。
頂點拓撲排序後,從前到後遍歷每一個頂點,於遍歷到頂點,其所有出邊到達頂點長度值。
如果求短路,本邊是短路徑一部分時。
求路反之。
[27]於有無環圖,短路需要複雜度
O
(
|
E
|
+
|
V
|
log
|
V
|
)
{\displaystyle O(|E|+|V|\log |V|)}
戴克斯特拉算法或
O
(
|
V
|
|
E
|
)
{\displaystyle O(|V||E|)}
貝爾曼-福特算法。
延伸閱讀…
[28]路徑是一個NP困難問題。
[29]
有無環圖偏序關係可以調度有着後順序限制系統任務中發揮作用。
[30]調度問題一個種類是串聯需要對象,如電子試算表中某個單元格計算公式依賴於其他單元格,或程序源代碼修改後編譯目標文件。
依賴圖(英語:dependency graph)記錄了這種依賴關係。
其每個頂點對應一個需要對象,邊則表示關係。
依賴圖中環被稱為環狀依賴(英語:circular dependency)。
環狀依賴是允許出現,因為不能保證圈內任務排定順序一致性。
無環依賴圖即為有無環圖。
[31]
舉例來説,電子表格中一個單元格數值發生改變,其他直接或間接依賴於該單元格所有單元格值需要計算。
調度任務計算某個單元格值。
一個單元格值取決於另外一個單元格時,兩個單元格之間有依賴關係。
每個依賴單元格值計算過程於使用它表達式執行。
使用依賴圖拓撲排序來調度任務使得每個單元格值計算一次情況下,整個工作表能。
[32]相似任務調度場景出現程序源代碼編譯makefile,[32]和優化計算機程序底層執行指令調度中。
[33]
我們知道,圖論 (Graph Theory) 起源是七橋問題,俗稱一筆畫問題。
這個問題後是大數學家尤拉 (Leonhard Euler, 1707/04/15-1783/09/18) 解決,開創了圖論這個領域。
圖組成元素有兩個:頂點 (vertex) 和 (edge)。
大學部圖論基本上只考慮圖,無論頂點是是集合。
數學上來説,我們定義 ,其中 代表頂點集 (Vertex Set),而集 (Edge Set) 是頂點集 Cartesian product 一個子集,而且是所謂 multiset,即裡面元素允許複計算。
確地説,每個有起點終點,如果有一個 起、是 這兩個頂點,我們可以寫成 ,這是什麼 會是 一個子集了。
而像這樣圖,邊本身具有方向性,因此稱有圖 (Directed Graph)。
舉例來説, 一個擁有兩個頂點、三個有圖。
但是,我們考慮七橋問題時,橋本身並沒有方向性,我們想要怎麼走哪個方向可以,這有了無向圖 (Undirected Graph) 誕生。
數學上於無圖定義: 無向圖若且唯若 if and only if 。
這個情況下,圖形上我們一條連接 兩個頂點直線來代表,並且畫上箭頭。
集合寫法部分,我們原本 兩個有方向性邊用 來表示。
上面這個有圖例子來説,我們可以發現實際上他會是一個無向圖;此時,它邊集表示方式可以簡化 。
我們説這個無圖只有兩個。
數學上,一個圖(Graph)是表示物件與物件之間關係方法,是圖論基本研究對象。
一個圖看起來是一些圓點(稱為頂點或結點)和這些圓點直線或曲線(稱為)組成。
如果圖每條規定一個方向,那麼得到圖稱為有圖,其邊稱為有邊。
有圖中,一個節點關聯有出邊和入邊分,而一個有關聯兩個點有始點和終點分。
相反,沒有方向圖稱為無向圖。
