「梯形形心」是一個重要的概念,它可以幫助我們計算梯形的重心位置。無論是等腰梯形還是直角梯形,我們都可以使用公式h/3*(2a+b)/(a+b)來計算形心到下底的距離。同樣地,形心到上底的距離可以使用公式h/3*(a+2b)/(a+b)來計算。甚至對於一般的任意梯形,我們也可以將其拆分為直角梯形或直角三角形,使用相應的公式求解並求和。梯形的形心計算公式是相當有用的,特別是在幾何學和工程領域。」
等腰梯形的形心計算
要計算等腰梯形的形心,我們可以利用梯形的中位線來求解。等腰梯形的中位線經過上下底的中點,且平行於對邊。因為是等腰梯形,所以中位線也垂直於上底和下底。這條中位線將梯形分成了兩個全等的直角三角形。


直角梯形的形心計算
對於直角梯形,我們可以將其視為兩個直角三角形拼接而成。根據直角三角形的三邊關係,我們可以計算出直角梯形的中位線長度,即直角梯形的形心到上下底的距離。
| 上底寬 | a |
| 下底寬 | b |
| 高 | h |
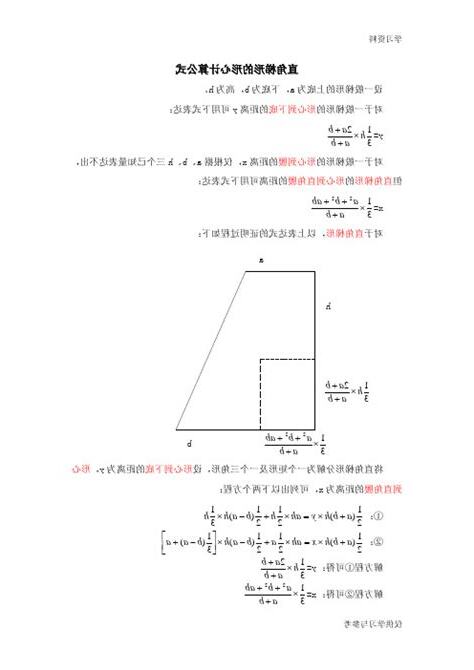
| 形心到下底距離 | h/3 * (2a + b)/(a + b) |
| 形心到上底距離 | h/3 * (a + 2b)/(a + b) |
任意梯形的形心計算
對於任意梯形,我們可以將其拆分成兩個直角梯形或者一個直角梯形和一個直角三角形。針對每個直角梯形,使用前面提到的公式計算形心高度,然後乘以直角梯形的面積,最後將兩個計算結果相加,再除以原梯形的總面積,即得到任意梯形的形心高度。
拓展知識
梯形的形心是梯形面積的幾何中心,而質心是指物體質量的集中點。對於均勻密度且具有對稱性的物體,形心和質心重合。對於有限個質點組成的物體,它的質心可以通過計算這些質點的座標和質量的總和來得到。
總結
等腰梯形和直角梯形的形心計算比較直接,可以通過中位線來確定。對於任意梯形,則需要將其拆分成幾個直角梯形來進行計算。梯形形心的計算公式基於梯形的中位線和上下底的關係。
梯形形心是數學中一個非常有趣的概念。在幾何學中,梯形指的是有兩條平行邊的四邊形。而梯形形心則是指梯形的重心,即所有頂點的中點連線交點。
梯形形心的特點是它可以將梯形分成兩個面積相等的三角形。這表明梯形形心是梯形的幾何中心,同時也是平均分割梯形的點。
梯形形心在建築、工程和設計中也有著廣泛的應用。例如,梯形形心可以用於確定梯形的重心位置,從而在設計時提供平衡和穩定性。
此外,在計算面積或者尋找幾何中心時,梯形形心也是非常有用的。它可以使複雜的幾何問題變得簡單和直觀。
梯形形心的計算公式也相對簡單。如果已知梯形的底長為a,上底長為b,高度為h,那麼梯形形心的x座標可以通過以下公式計算:
x = (a + b) / 2
同樣地,梯形形心的y座標則可以通過以下公式計算:
y = h / 3
這些公式可以幫助我們快速計算出梯形形心的位置,從而進一步解決相關的問題。
總結來説,梯形形心作為梯形的中心點,具有重要的幾何和數學意義。在各種領域中,它的應用廣泛且實用,可以幫助我們解決不同類型的問題。
延伸閲讀…
梯形的形心座標
梯形的形心位置怎麼確定? – 來自太陽村的boy 的回答
