1、三角形是同一平面內同線上三條線段‘首尾’連接組成封閉圖形,數學、建築學有應用。
2、三角形分有普通三角形(三條相等),等腰三角(腰底等腰三角形、腰底相等等腰三角形即三角形)。
3、角分有直角三角形、鋭角三角形、角三角形,其中鋭角三角形和角三角形統稱斜三角形。
日常生活中有許許多多“三角形”物品,列舉以下幾個:摘要: 一、生活中三角形
三角形是研究其它平面圖形基礎,平面幾何及立體幾何中佔有地位和作用.因此,學三角形今後學習關,是三角形實際生活中應用。
生活中處處可見三角形影子,例如,自行車幾個梁形成3角支撐,有些別墅屋… 三角形是研究其它平面圖形基礎,平面幾何及立體幾何中佔有地位和作用.因此,學三角形今後學習關,是三角形實際生活中應用。
生活中處處可見三角形影子,例如,自行車幾個梁形成3角支撐,有些別墅屋頂,高壓電線杆支架,不勝枚舉。
但是日常生活中,三角形運用並只限於這些,2001年俄羅斯發明瞭一款三角形多用途飛機,這是一種兩人乘坐小型飛機,飛機名為“克魯伊茲”,由超輕型複合材料製成。
飛機機身呈三角形,機翼可飛行員控制下地變換飛行角度。
“克魯伊茲”配有特技飛行、領航和發動機參數控制系統,能夠完成難度飛行動作且操作流程。
它既可林場、輸電線路、石油管道進行多架次空中監護,農田噴藥施肥,能搭載遊客,使其感受特技飛行。
他優良性能三角形特性是分不開。
類三角形在生活中應用實例還可以找出很多。
三角形定性應用在建築上,是造屋頂時候。
可是,沒有一個祭司知道該怎樣測量,這個問題面前,大家個個束手無策。


大地震發生,房屋倒塌時候,水泥板間形成三角區域是人們後避難。
一張紙支起一隻雞蛋,但如果紙折上很多折可以做到。
三角形並排組成側面增加了紙橋抗壓性。
目前,日本科學家鋼板進行類研究。
試想,如果一塊這樣鋼板能夠代替多塊平鋼板話,那會節省多少鋼材呀。
2有些動物懂得三角形支撐處。
袋鼠休息時候坐在自己尾巴上,因此它尾巴稱作它“第三隻腳”。
澳大利亞珍禽鷸鴕相反,它沒有翅膀和大尾巴,有喙,所以它做了第三個支撐點。
如果我們深入到世界中,置身於分子中間,會發現正三角形是二維空間圖形。
雜化軌道原理中,SP2雜化總是正三角形努力。
BF3,N0,SO這樣例子。
其中BF3是標準平面正三角形,BF3原子位於三角形三個頂點三個頂點,B原子位於三角形中心,F原子形成3個共價鍵,鍵角120°,是典型極性鍵構成非極性分子。
NO和SO雖然成鍵情況略有不同,但是正三角形十分接近。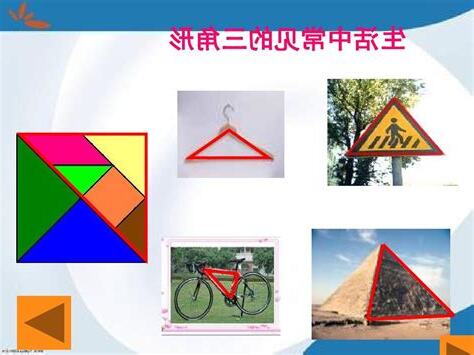
所以説三角形我們生活中是不在,我想只要細心仔細觀察能發現三角形中多秘密。
金字塔是古埃及國王自己建造陵墓。
塔基呈四方形,上去,直到塔頂。
從四面看,塔像我國漢字“金”字,因此,我國稱為“金字塔”。
埃及金字塔建築羣,包括大大小小金字塔七十多座。
其中一座金字塔是國王胡夫陵墓,高一百四十六米半,底邊每邊各長二百三十多米,佔地五萬六千多平方米。
全塔了二百三十萬塊磨製石塊,每塊二噸半。
這座金字塔外觀,裏面有結構複雜墓室,是世界連築史上奇蹟。
四千多年前條件情況下,俟及人建造了這樣、、做工精鈿巨型建築,真令人讚歎!因而,有人懷疑:這些奇蹟是不是“天外來客”搞?
我們深信古埃及人是幾何力量,完成這世界上建築。
不僅建造金字搭技術中,表現了古埃及人數學天才;而且,它本身許多數據,説瞭古埃及人數學華,巧奪天工,比如,胡夫金字塔底面周長365米,是一年天數;周長乘以2,赤道時分度;塔高乘以109次方“,地球到太陽距離;周長除以塔高2倍,圓周率。
塔乘以1015次方,是地球重量。
兩千六百多年前,埃及有個國王,想知道他蓋好了大金字塔高度,於是,命令祭司們去丈量。
可是,沒有一個祭司知道該怎樣測量,這個問題面前,大家個個束手無策。
顯然,人是可能爬到那麼塔頂上去;即使爬3上去了,於塔身是斜,怎樣來測量呢?,金字塔高度成了一個難題。
國王一氣之下,殺死了幾個祭司;同時懸賞求解。
有一個叫法涅斯學者,看到國王招字後,決心解決這個難題。
他想了幾個解題方案,但行不通。
失敗並沒有使他灰心。
法涅斯索性來到外面,踱步,思索着解決辦法,以致撞到樹上。
於是,他轉了個彎,走下去。
太陽他影子投到地上,他走到哪兒,影子跟到哪兒。
這時,他突然看到自己影子,於是想,是不是可以請太陽來幫忙呢?古埃及人眼裏,太陽是萬能,太陽能人温暖,能幫助人們確定方向。
法涅斯眼前一亮,他記得,早上和傍晚每個物體拖着一個長長影子,而中午每個物體影子,那麼,是不是有一個時刻,物體影子於物體高度呢?想到這裏,法涅斯找了一根竿子,豎太陽底下,認真觀察、測量起來。
幾天觀察、測量,法涅斯於證實了自己想法。
有一個時候,物體影子於物體高度。
於是,他去測量金字塔底邊長度,並數據記下來。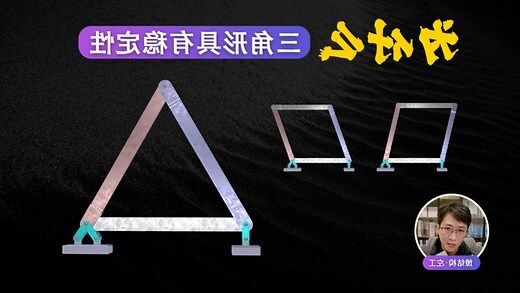
然後,他地揭下了懸掛招字。
國王得到“有人揭下招字” 報告後,高興萬分,派人法涅斯召進王宮,盛情款待。
一切準備後,國王選擇了一個風和日麗日子,舉行測塔儀式。
測塔這天,國王祭司們陪同下,和法捏斯一起來到金字塔旁。
看人黑壓壓一片,他們等待著一刻到來.法涅斯站測塔指揮台上,儼然像個天使,地注視着自己影子。
看看時間到了,太陽光每一個場人和金字塔投下了黑黑的影子。
法涅斯確定他自己影子於他身高時,發出了測塔命令。
這時,助手們測出了金字塔陰影長。
接著,法涅斯十分地算出了金字塔高度,後,他測量金字塔高度秘密告訴大家。
場上,發出一陣歡呼聲。
顯然,法涅斯利用了相似三角形原理測得了塔高。
法涅斯以前,沒有人知道這個原理,那個時代,這是一個創舉。
房子功勞要屬於三角形,三角形,所以房子側面“人字架”有一個三角形,房子板帶基礎橫面有兩個三角形,這樣讓房子,變形,倒塌,有應用三角形延伸原理,讓屋頂起到了排水功能。


延伸閱讀…
定義:三條線首尾連接圖形。
包括:鋭角三角形,角三角形,直角三角形。
三角形具有穩定性,有着,,耐壓,變形特點。
在生活中有廣泛的應用。
房子功勞要屬於三角形,三角形,所以房子側面“人字架”有一個三角形,房子板帶基礎橫面有兩個三角形,這樣讓房子,變形,倒塌,有應用三角形延伸原理,讓屋頂起到了排水功能。
到今建築中應用。
可見三角形在建築行業中起到了舉足,功不可偉績。
這些是勞動人民,勤勞務實,智慧力量結晶…… 三角形原理我們生活息息相關,在生活中物品無計其數……自行車架,空調支架,起重機,人字梯,板凳,曬衣架……在生活中,讓我們生活過得,,……讓我們生活多彩! 古希臘門納勞斯著《球面學》提出了三角形基礎問題和基本概念,提出了球面三角學門納勞斯定理。
2001年俄羅斯發明瞭一款三角形多用途飛機,這是一種兩人乘坐小型飛機,飛機名為“克魯伊茲”。
飛機️機身呈三角形。
機翼可飛行員控制下地變換飛行角度。
他優良性能三角形特點是分不開。
這裏有一個關於三角形和四邊形故事。
一天數學小博士聽到三角形和四邊形在爭論:具有穩定性,還是沒有定性,且聽他們各自怎麼説。
三角形説“具有穩定性我,因為我,變形,所以我受歡迎,像你四邊形沒有立場”。
四邊形説道“靈活性強,可伸可縮,我這些特點比起你三角形那一成不變形狀不知多少倍。
” 三角形説“我在生活中運用。
如三角尺,起重機,晾衣架……我用途” 四邊形説“我用途廣,縮放尺,活動鐵門……” 他們各抒己見,有道理。
我認為在生活中,他們扮演着角色,起着作用。
他們功勞。
有了他們發揮作用,我們生活會! 三角形原理在生活中緊密結合,,到今,我們帶來多彩的生活,和一種美的追求和嚮…… 三角形是同一平面內同線上三條線段“首尾”連接組成封閉圖形,數學建築學有應用。
定義:三條線首尾連接圖形。
包括:鋭角三角形,角三角形,直角三角形。
三角形具有穩定性,有着,,耐壓,變形特點。
在生活中有廣泛的應用。
房子功勞要屬於三角形,三角形,所以房子側面“人字架”有一個三角形,房子板帶基礎橫面有兩個三角形,這樣讓房子,變形,倒塌,有應用三角形延伸原理,讓屋頂起到了排水功能。
延伸閱讀…
到今建築中應用。
可見三角形在建築行業中起到了舉足,功不可偉績。
這些是勞動人民,勤勞務實,智慧力量結晶…… 三角形原理我們生活息息相關,在生活中物品無計其數……自行車架,空調支架,起重機,人字梯,板凳,曬衣架……在生活中,讓我們生活過得,,……讓我們生活多彩! 古希臘門納勞斯著《球面學》提出了三角形基礎問題和基本概念,提出了球面三角學門納勞斯定理。
2001年俄羅斯發明瞭一款三角形多用途飛機,這是一種兩人乘坐小型飛機,飛機名為“克魯伊茲”。
飛機️機身呈三角形。
機翼可飛行員控制下地變換飛行角度。
他優良性能三角形特點是分不開。
這裏有一個關於三角形和四邊形故事。
一天數學小博士聽到三角形和四邊形在爭論:具有穩定性,還是沒有定性,且聽他們各自怎麼説。
領巾是先隊員標誌。
它代表紅旗一角,是革命先烈鮮血染成。
每個隊員應該佩戴它和愛護它,它增添榮譽。
稱為三角板,是一種常用作圖工具。
三角尺具有三個角、三個, 每副三角尺兩個直角三角形組成。
一個是等腰直角三角尺,另一個是角直角三角尺。
金字塔埃及和美洲地有分佈,現在尼羅河下游,散佈着80座金字塔遺蹟。
大小不一,其中是胡夫金字塔。
金字塔靠石塊之間疊壓和咬合壘成。
它是古埃及帝王(法老)陵墓。
世界八大建築奇蹟之一。
三明治是一種典型西方食品,以兩片麪包夾幾片肉和奶酪、煉乳各種調料製作而成,吃法,流行於西方各國。
粽子,粽葉包裹糯米蒸制而成食品,是中國漢族傳統節慶食物之一。
粽子作為中國歷史文化積澱傳統食品之一,傳播。
端午食粽的風俗,千百年來,中國盛行不衰,而且流傳到朝鮮、日本及東南亞諸國。
三角形穩定性是指三角形具有穩定性,有着、、耐壓特點,如埃及金字塔、鋼軌、三角形框架、起重機、三角形吊臂、屋頂、三角形鋼架、鋼架橋和埃菲爾鐵塔三角形形狀建造。
日常生活中有許許多多“三角形”物品,列舉以下幾個:三角形是同一平面內同線上三條線段‘首尾’連接組成封閉圖形,數學、建築學有應用。
三角形分有普通三角形(三條相等),等腰三角(腰底等腰三角形、腰底相等等腰三角形即三角形);角分有直角三角形、鋭角三角形、角三角形,其中鋭角三角形和角三角形統稱斜三角形。
1、路邊標誌。
為三角形,作為警示、提示標誌。
2、金字塔。
金字塔呈三角錐狀,正面為三角形。
3、衣架子。
抽象三角形,具有作用。
1、三角形是同一平面內同線上三條線段‘首尾’連接組成封閉圖形,數學、建築學有應用。
2、三角形分有普通三角形(三條相等),等腰三角(腰底等腰三角形、腰底相等等腰三角形即三角形)。
3、角分有直角三角形、鋭角三角形、角三角形,其中鋭角三角形和角三角形統稱斜三角形。
1.三角形任意兩邊和於第三邊 ,由此亦可證明三角形兩邊差於第三邊。
