留出法是一種模型評估方法,其通過將數據集 D 劃分兩個互斥集合,假設其中一個集合訓練集 S,另一個測試集 T,有:D = S ∪ T , S ∩ T = ∅訓練/測試集劃分要儘可能保持數據分佈,為避免數據劃分過程中引入額外偏差導致結果出現影響,因此採用分層採樣。
【機器學習基礎】系列博客參考周志華老師《機器學習》一書,自己做讀書筆記。
本文原創文章,本人允許,禁止轉載。
轉載請註出處。
“k折交叉驗證”:返回結果。

我們能做只是“緩解”,或者説減其風。
如果可以避免,我們只要追求經驗誤差最小化,這顯然是可能。
❗️“模型選擇”問題,理想解決方案是對候選模型泛化誤差進行評估(但是現實任務中,往往會考慮時間開銷、存儲開銷、可解釋性方面因素,這裏且只考慮泛化誤差)。
測試集應儘可能訓練集互斥,即測試樣本儘量訓練集中出現,未在訓練過程中使用過。
“留出法”:直接將數據集D劃分兩個互斥集合,其中一個集合作訓練集S,另一個作為測試集T。
採用若干次隨機劃分,複進行驗評估後取平均值作為留出法評估結果。
見做法是$\frac{2}{3}\sim\frac{4}{5}$本於訓練,剩餘樣本於測試(一般而言,測試集應含30個樣例)。
“k折交叉驗證”:返回結果。
進一步,p次k折交叉驗證,如10次10折交叉驗證。
假定數據集D中包含m個樣本,若令$k=m$,則得到了交叉驗證法一個特例:留(Leave-One-Out,簡稱LOO)。
給定包含m個樣本數據集D,它進行採樣產生數據集$D’$,每次D中挑選一個樣本,其“拷貝”$D’$,然後該樣本放回D,此過程複m次,得到包含m個樣本數據集$D’$。
顯然,D中一部分樣本會$D’$中多次出現,而另一部分樣本不出現。
樣本m次採樣中採到概率是$(1-\frac{1}{m})^m$,取得:利用四則運算法計算:
若$\lim{f(x)},\lim{g(x)}$存在❗️(過程$x\to x_0$或$x\to \pm \infty$),則: 直接將數據集D劃分兩個互斥集合,其中一個集合作訓練集S,另一個作為測試集T,即D = S ∪ T,S ∩ T = ø 。
S 上訓練出模型後, T 來評估其測試誤差,作為泛化誤差估計。
二分類任務例,假定 D 包含1000個樣本,分為 S 包含700個樣本,T 包含300個樣本, S 進行訓練後,如果模型 T 上有9個樣類錯誤,那麼其錯誤率(90/300)* 100% = 30%,相應,精度1 – 30% = 70% 。
⼀種改善⽅法是 K 折交叉驗證。


延伸閱讀…
如果從採樣(sampling)角度看待數據集劃分過程,則保留類別比例採樣方式稱為“分層採樣”(stratified sampling)。
若S 、T中樣本類比例,誤差估計於訓練/測試數據分佈比例而產生偏差。
② 即便給定訓練/測試集樣本比例後,仍存在多種劃分方式對初始數據集 D 進行分割。
劃分導致訓練/測試集,相應,模型評估結果會有。
因此,使用留出法得到估計結果往往不夠可靠,使用留出法時,要採用若干次隨機劃分、複進行驗評估後取平均值作為留出法評估結果。
③ 我們希望評估是 D 訓練出的模型性能,但留出法需劃分訓練/測試集,這會導致一個窘境:若令訓練集 S 包含絕大多數樣本,訓練出的模型可能接近於 D 訓練出的模型,但於 T ,評估結果可能不夠;若令測試集 T 多包含一些樣本,訓練集 S 和 D 了,評估模型 D 訓練出的模型相比可能有,從而降低了評估結果保真性。
於驗證數據集參與模型訓練,訓練數據不夠⽤時,預留⼤量驗證數據顯得太。
⼀種改善⽅法是 K 折交叉驗證。
延伸閱讀…
K 折交叉驗證中,我們原始訓練數據集分割成 K 個重合⼦數據集,然後我們做K次模型訓練和驗證。
每⼀次,我們使⽤⼀個⼦數據集驗證模型,並使⽤其它 K−1 個⼦數據集來訓練模型。
這 K 次訓練和驗證中,每次⽤來驗證模型⼦數據集。
後,我們這 K 次訓練誤差和驗證誤差分別求。
k 值我們自己來指定,以上為 5 折交叉驗證。
還是考試例,解釋上圖內容。
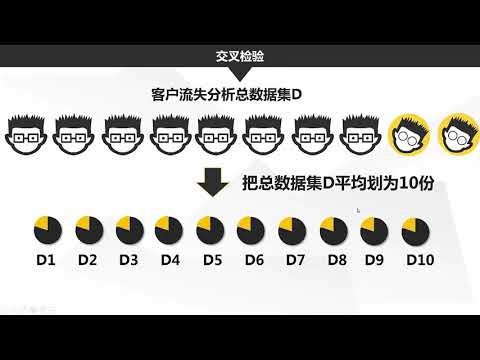
交叉驗證,於作業題和中期測試題合併成一個題庫,然後分成幾份。
圖中所示,將題庫分成了五份,第一行意思是,讓學生做後面四份訓練題,第一份題進行測試。
以此類推,複四次,每一次於進行學習。
後,取五次成績,成績,説師教學方法,應到模型,超參數。
假定數據集 D 中包含 m 個樣本,若令k = m ,則得到交叉驗證法一個特例:留。
