相似性質有哪些?相似三角形是指具有相同內角的三角形,且對應邊成比例。它們之間的相似比記為1。當兩個三角形具有對應邊成比例且夾角相等時,它們是相似的。另外,若兩個三角形的三條邊對應成比例,它們也是相似的。如果兩個三角形中有一組角對應相等,且夾角相等,則這兩個三角形相似。
相似三角形的定義與性質
在幾何學中,兩個三角形如果滿足以下條件之一,則被稱為「相似三角形」:
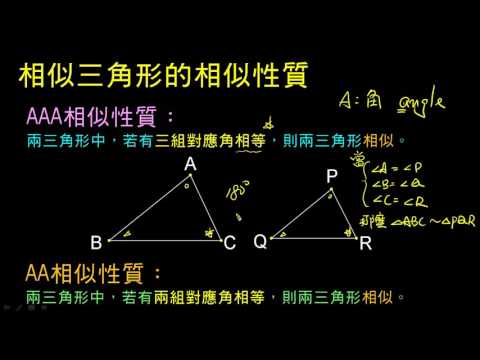

- 1. 對應的角(不是邊)相等。
- 2. 對應的邊(不是角)成比例。
相似比與全等三角形
當兩個三角形相似時,它們的對應邊之比稱為相似比。如果兩個三角形的相似比為 1,則它們是完全相同的,這意味著它是全等三角形。
相似三角形的性質
-
如果兩個三角形的兩組對應邊長成比例,並且夾角相等,那麼這兩個三角形相似。這一性質被稱為「$ASA$ 相似性質」。例如,當 $\angle A = \angle P$ 且 $\overline{AB} : \overline{PQ} = \overline{AC} : \overline{PR}$ 時,則 $\triangle ABC \sim \triangle PQR$。
-
如果一個三角形的三條邊與另一個三角形的三條邊對應成比例,那麼這兩個三角形相似。這一性質稱為「$SSS$ 相似性質」。例如,當 $\overline{AB} : \overline{PQ} = \overline{AC} : \overline{PR} = \overline{BC} : \overline{QR}$ 時,則 $\triangle ABC \sim \triangle PQR$。
$SAS$ 相似性質
如果兩個三角形中有一組角對應相等,且夾這組等角的兩組邊長對應成比例,則這兩個三角形相似,此性質稱為「$SAS$ 相似性質」。例如,當 $\angle A = \angle P$ 且 $\overline{AB} : \overline{PQ} = \overline{AC} : \overline{PR}$ 時,則 $\triangle ABC \sim \triangle PQR$。
實例解析
根據 $SAS$ 相似性質,如果一個三角形的一個角和另一個三角形的一個角對應相等,並且夾這兩個角的兩條邊長對應成比例,那麼這兩個三角形相似。在給定的例子中,$\angle A = \angle P$ 且 $\overline{AB} : \overline{PQ} = \overline{AC} : \overline{PR}$,因此滿足了 $SAS$ 相似性質的條件,所以 $\triangle ABC \sim \triangle PQR$。
| 條件 | 結果 |
| $\angle A = \angle P$ | 相同的角度 |
| $\overline{AB} : \overline{PQ} = \overline{AC} : \overline{PR}$ | 比例邊 |
| 相似三角形 |
相似三角形是幾何學中一個重要的概念,它們在測量、建築設計和工程計算中都有應用。在測量不便於直接測量的距離時,通過相似三角形的性質可以間接計算出目標距離。
“`
相似性質有哪些
相似性質是指事物之間的共同特徵或相似點。在各個領域中,我們可以找到許多不同事物之間的相似性質。以下是一些常見的相似性質:
1. 形狀相似性質
形狀相似性質是指不同事物在外觀方面的相似點。例如,兩個石頭可能具有相似的圓形或方形外觀。這種相似性質在幾何學和設計領域中非常常見。
2. 功能相似性質
功能相似性質是指不同事物在功能上的相似點。例如,手機和平板電腦具有相似的功能,都可以用來瀏覽網頁、播放影片等。這種相似性質在科技產品中常見。
3. 物質相似性質
物質相似性質是指不同事物所使用的物質相似。例如,玻璃杯和玻璃瓶都是使用玻璃製成的,具有類似的物質結構和性質。這種相似性質在材料科學和化學領域中研究。
4. 行為相似性質
行為相似性質是指不同事物在行為模式上的相似點。例如,動物之間可能具有類似的捕食方式、遷徙模式等。這種相似性質在生物學和行為科學中研究。
5. 文化相似性質
文化相似性質是指不同事物在文化背景下的相似點。例如,不同國家之間可能存在相似的傳統節日、飲食習慣等。這種相似性質在人類學和社會學中研究。
6. 結構相似性質
結構相似性質是指不同事物在組織結構上的相似點。例如,一個公司和一個政府部門都具有類似的組織結構,包括不同層級的管理和職能分工。這種相似性質在組織學和管理學中研究。
7. 屬性相似性質
屬性相似性質是指不同事物所具有的屬性相似。例如,兩個人可能具有相似的年齡、性別和職業等屬性。這種相似性質在統計學和人口學中研究。
綜上所述,相似性質是指不同事物之間的共同特徵或相似點,在各個領域中都有廣泛應用。相似性質的研究可以幫助我們更好地理解不同事物之間的關係,促進知識的交流和創新的發展。
延伸閲讀…
三角形相似性質
相似三角形- 維基百科,自由的百科全書
