磁場(magnetic field)是一向量場,其描述於移動電荷、電流[1][2]、磁性材料磁影響(磁效應、磁作用)。
磁場中移動電荷會受到垂直於其自身速度和垂直於磁場力[3]。
電磁學裡,磁石、磁鐵、電流及時變電場,會產生磁場[4][5]。
處於磁場中磁性物質或電流,會因為磁場作用而感受到磁力,因而顯示出磁場存在。
磁場是一種向量場;磁場空間裡任意位置具有方向和數值大小[notes 1]。
磁鐵磁鐵之間,透過各自產生磁場,施加作用力和力矩於方。
運動中電荷會產生磁場。
磁性物質產生磁場可以電荷運動模型來解釋[notes 2]。
當施加外磁場於物質時,磁性物質內部會磁化,會出現很多微小磁偶極子。
磁化強度估量物質磁化程度。
知道磁性物質磁化強度,可以計算出磁性物質本身產生磁場。
產生磁場需要輸入能量,磁場湮滅時,這能量可以回收利用,因此,這能量視為儲存於磁場。
電場是電荷產生。
電場磁場有密切關係;時變磁場會生成電場,時變電場會生成磁場。
馬克士威方程組描述電場、磁場、產生這些向量場電流和電荷,這些物理量之間詳細關係。
狹義論,電場和磁場是電磁場兩面。
設定兩個參考系A和B,於參考系A,參考系B速度移動。
參考系A觀察靜止電荷產生電場,參考系B觀察成為移動中電荷產生電場和磁場。
量子力學中,科學家認為,磁場電場是光子所造成效應。
標準模型術語來表達,光子是所有電磁作用顯現依賴媒介。
於大多數場景,無需使用描述,使用經典理論;低場能量狀況,其中是可以。
古今社會裡,很多對世界文明有貢獻發明涉及到磁場概念。
地球能夠產生自己磁場,這導航方面,因為指南針指北極地指向位置地球地理北極附近地磁北極。
電動機和發電機運作機制是倚賴磁鐵轉動使得磁場隨著時間而改變。
通過霍爾效應,可以給出物質帶電粒子性質。
磁路學專門研討,各種各樣像變壓器一類電子元件,其內部磁場相互作用。
磁場於周圍環境影響,可以幾種價方法來定義磁場。
例如,類似於電場,磁場電荷會施加作用力;但電場是,它移動中電荷施加作用力,而且作用力方向垂直於磁場本身和電荷速度。
繪製場線圖是一種簡、描述磁場(或任意其它向量場)方法,空間任意位置磁場可以場線圖對應位置場線正切方向和密度估計出來。


德馬立克仔細標明瞭鐵針塊型磁石附近各個位置定向,這些記號,描繪出很多條磁場線。
他發現這些磁場線會於磁石相反兩端位置,好像地球經線相會於南北極。
因此,他稱這兩位置磁極[6]。
三個世紀後,威廉·吉爾伯特主張地球本身一個磁石,其兩個磁極位於南北極。
出版於1600年,吉爾伯特鉅著《論磁石》(De Magnete)開創磁學一門正統科學學術領域。
於1824年,西莫恩·帕松發展出一種物理模型,能夠描述磁場。
帕松認為磁性是磁荷產生,同類磁荷相排斥,異類磁荷相吸引。
他模型完全類現代靜電模型;磁荷產生磁場,電荷產生電場。
這理論能夠正確地預測儲存於磁場能量[notes 4]。
儘管帕松模型有其之處[notes 5],這模型有兩點瑕疵。
第一,磁荷並存在。
將磁鐵切為兩半,並會造成兩個分離磁極,所得到兩個分離磁鐵,每一個有自己指南和指北極。
第二,這模型不能解釋電場磁場之間關係。
於1820年,一系列革命性發現,促使開啟了現代磁學理論。
,丹麥物理學家漢斯·奧斯特於7月發現載流導線電流會施加作用力於磁針,使磁針轉指向。
後,於9月,這新聞抵達法國科學院一週後,安德烈-瑪麗·安培地做實驗展示出,假若所載電流流向,兩條平行載流導線會吸引;否則,假若流向相反,會排斥。
緊接著,法國物理學家讓-巴蒂斯特·歐和菲利克斯·沙伐於10月發表了歐-沙伐定律;這定律能夠正確地計算出在載流導線四周磁場。
1825年,安培發表了安培定律。
這定律能夠描述載流導線產生磁場。
,這定律幫助建立整個電磁理論基礎。
於1831年,麥可·法拉第證實,隨著時間而變化磁場會生成電場。
這實驗結果展示出電磁之間密切關係。
1861年到1865之間,詹姆斯·馬克士威經典電學和磁學雜亂無章方程式加以整合,發展馬克士威方程組。
發表於他1861年論文《論物理力線》,這方程組能夠解釋經典電學和磁學各種現象。
論文裡,他提出了「分子渦流模型」,並地將安培定律加以延伸,增加入了一個有關於位移電流項目,稱為「馬克士威修正項」。
於分子渦包具有彈性,這模型可以描述電磁波物理行為。
因此,馬克士威推導出電磁波方程式。
他計算出電磁波傳播速度,發現這數值光速接近。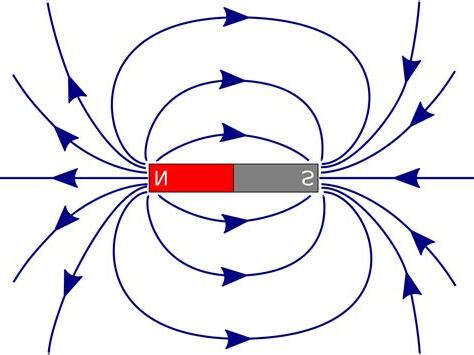
警覺馬克士威斷定光波一種電磁波。
後來,於1887年,海因裏希·赫茲做實驗證明瞭這事。
馬克士威統一了電學、磁學、光學理論。
雖然,有了具功能馬克士威方程組,經典電動力學基本上完備,理論方面,二十世紀帶來了多改良與延伸。
阿爾伯特·愛因斯坦,於1905年,他論文裡表明,電場和磁場是處於參考系觀察者觀察到同樣現象(幫助愛因斯坦發展出狹義相對論思想實驗,關於其細節,請參閲移動中磁鐵導體問題)。
後來,電動力學量子力學合併量子電動力學。
各個學術領域裡,磁場會用來稱呼兩種向量場,標記
H
{\displaystyle \mathbf {H} }
和
B
{\displaystyle \mathbf {B} }
:
雖然「磁場」這個詞彙歷史上H場佔有,而只能B場稱「磁感應」,但是現在多數物理學家公認B場為基本物理量,因此他們稱呼B場「磁場」[notes 6],電機電子工程師學會(IEEE)H場定義「磁場」,B場定義「磁通量密度」[8]。
命名表格展示,B場和H場習慣命名並不一致。
分歧義,本文章裏,磁感應強度指是B場,磁場強度指是H場,而磁場上下文而定,指是B場。
其中,
μ
0
{\displaystyle \mu _{0}}
是磁常數,
M
{\displaystyle \mathbf {M} }
是磁化強度。
於線性物質,磁化強度
M
{\displaystyle \mathbf {M} }
B場成正比,所以,B場H場之間關係
其中,
μ
′
{\displaystyle \mu ‘}
是磁導率。
空間裏,磁化強度於零,所以,
於很多其它物質,磁化強度B場之間關係複雜。
例如,鐵磁性物質和超導體磁化強度是
B
{\displaystyle \mathbf {B} }
多值函數(multivalued function)。
這現象稱為現象[10]。
國際位制裡,B場單位特斯拉(tesla),價於韋伯(weber)/平方米,或伏特·秒/平方米。
CGS單位制裡,B場單位高斯(gauss)。
1特斯拉於10,000高斯。
國際位制裡,H場單位安培/公尺;CGS單位制裡,H場單位奧斯特(oersted)。
1奧斯義
1000
/
4
π
≈
79.5774715
{\displaystyle 1000/4\pi \approx 79.5774715}
安培/公尺[11]。
儀器能夠測量到微小磁場數量級阿託特斯拉(10−18特斯拉)[12];實驗室能夠製備磁場2800特斯拉[13]。
很多像磁星一類天文星體,其磁場值域0.1100吉咖特斯拉(1081011特斯拉),超強於實驗室磁場[14]。
磁強計(magnetometer)是測量局域磁場儀器。
磁強計分為很多類,幾類包括霍爾效應磁強計、超導磁強計、核子旋進磁力儀(NMR magnetometer)、磁通門磁強計(fluxgate magnetometer)。
天文星體磁場可以靠著測量其於附近帶電粒子影響而得知。
例如,繞著磁場線螺旋轉動電子會產生輻射,其無線電波數據可以電波望鏡偵測獲得。
磁場方向可以藉著磁偶極子性質來顯示,處於磁場磁偶極子會沿著磁場磁場線平行排列,其中一個顯著例子磁鐵周圍鐵粉分佈圖案。
條狀磁鐵放在白紙下面,鋪灑一堆鐵粉白紙上面,這些鐵粉會依著正切磁場線方向排列,形成一條條曲線,曲線每一點顯示出磁場線正切方向。
這曲線圖稱為「場線圖」。
繪製場線圖是一種簡、描述磁場(或任意其它向量場)方法,空間任意位置磁場可以場線圖對應位置場線正切方向和密度估計出來。
磁場線密度表示磁場。
場線圖繪製。
,每一個位置測量磁場數值大小和方向。
所得數據,圖紙對應位置繪出一條磁場同方向箭桿。
然後,每條箭桿首部與前面箭桿尾部連接起來,形成磁場線,確使磁場線密度磁場強度成正比。
這樣,可以繪製出場線圖。
這是一種磁場視覺化方法。
想像磁場線會沿著線徑施加張力(像一條橡皮圈),會垂直於線鄰近磁場線施加壓力,這磁力物理行為。
兩塊磁鐵異性磁極吸引,這是於它們很多條磁場線結;反之,兩塊磁鐵同性磁極排斥,這是於它們磁場線相交接,因為平行,造成推擠。
磁場任意位置方向可以指南針來顯示。
指南針可以顯示出一個條形磁鐵磁場方向。
於異性磁極吸引,指南針指北極會磁鐵指南極(S)吸引;於同性磁極排斥,指南針指北極會磁鐵指北極(N)排斥。
磁鐵指南極附近,磁場指向磁鐵;指北極附近,磁場背向磁鐵。
載流導線產生磁場會指向導線,會背向導線,而會環繞著導線。
出現於地球北極高空或南極高空極光可以顯示出磁場線。
太陽流出來大量離子形成了太陽風,其中一部分會流往地球,地球高空,地球磁場捕獲,沿著磁場線集中北極高空南極高空。
這些離子氣層原子、分子之間碰撞,造成了能量極光形式釋出。
,極光看起來像是漫射(diffusion)輝光(glow)或「光簾」,著東-西方延伸。
每一張光簾是許多條平行射線組成。
每一條射線那位置磁場線同方向。
這令人覺得光是地球磁場塑造成形。
確實無誤,從人造衞星觀察證了離子磁場線引導,繞著磁場線盤,朝著地球移動。
繪製場線圖是一種有用表示向量場方法,可以地顯示出向量場緻屬性。
磁場一個性質可以用場線圖顯示出來:磁場線沒有初始點,結點;磁場線會形成閉迴路,或無窮遠延伸無窮遠。
,科學家發現任何例外。
磁場是一種螺線向量場。
磁場線會磁鐵指北極附近離開磁鐵,會磁鐵指南極附近進入磁鐵;磁鐵內部,磁場線指南結至指北極[notes 7]。
任何一條進入磁鐵磁場線會磁鐵出來;絕不容許磁場線終結於任何位置。
磁極總是指北極和指南形式出現。
將磁鐵切為兩半,會形成兩塊磁鐵,其中每一塊磁鐵擁有自己指北極和指南極。
正式而言,所有進入某區域磁場線,離開那區域。
因此,進入某區域磁場線數目[notes 8],減去離開那區域磁場線數目,結果於零。
這結果稱為高斯磁定律,方程式表示:
其中,
S
{\displaystyle \mathbb {S} }
是閉曲面,
d
a
{\displaystyle \mathrm {d} \mathbf {a} }
是微小面元素。
磁性物質外面,H場線B場線等同;但磁性物質內部,H場B場數值大小、方向可能,這依賴磁化強度
M
{\displaystyle \mathbf {M} }
而定,這關係可以由H場定義方程式看出來:
設外磁場於零,一個磁鐵內部,B場H場呈相反方向。
H場線開始於指北極,終結於指南極。
相與,B場線形成一個閉迴圈,磁鐵內部,從指南延續到指北極,磁鐵外部,指北極繞道指南極。
H場線電場線類;電場線開始於正電荷,終結於負電荷。
這使人想要處於兩端局域磁荷磁鐵模型。
很可惜地,這磁荷模型並確,是計算磁鐵內部磁場時。
例如,參閲右圖,採用原子尺寸載流迴圈模型來描述,一個磁化強度
M
=
M
z
^
{\displaystyle \mathbf {M} =M{\hat {z}}}
磁性球體,價於一個滿足以下條件球體:內部束縛電流密度
J
b
{\displaystyle J_{b}}
和表面束縛電流密度
K
b
{\displaystyle K_{b}}
其中,
n
^
{\displaystyle {\hat {n}}}
是垂直於球體表面的徑向單位向量。
一番運算,可以得到,表面束縛電流密度為
M
sin
θ
{\displaystyle M\sin \theta }
球體,其內部B場
H場
H
{\displaystyle \mathbf {H} }
定義式,
所以,磁化球體內部,B場H場呈相反方向[15]。
磁單極子是一種假想粒子(或粒子類),這粒子擁有一個磁極(指北極或指南極)。
換句話説,類似帶電粒子擁有電荷,磁單極子擁有磁荷。
現今,於這概念興趣大多出自於粒子物理學,值得注意的是大統一理論和超弦理論,關於磁單極子存在或可能性,它們做了很多預測,因而激發出許多物理學者尋找磁單極子。
但儘管竭盡全力,物理學者無法觀察到任何磁單極子蛛絲馬跡[notes 9]
進研究發現自旋冰(spin ice)是一種可以模擬磁單極子材料,但含有磁單極子。
設一個平面載流迴圈面積向量為
a
{\displaystyle \mathbf {a} }
、所載電流
I
{\displaystyle I}
,其磁偶極矩
μ
{\displaystyle {\boldsymbol {\mu }}}
方向,右手法則,是大拇指載流迴圈平面指出方向,而其它拇指指向電流流動方向,磁偶極矩大小於電流乘以迴圈面積。
方程式表示,磁偶極矩
μ
{\displaystyle {\boldsymbol {\mu }}}
為
這面積載流迴圈有階磁矩,像磁四極矩,磁八極矩。
設載流迴圈面積趨於零、電流趨向於無,同時保持
μ
=
I
a
{\displaystyle {\boldsymbol {\mu }}=I\mathbf {a} }
不變,則所有階磁矩會趨向於零,這載流迴圈趨於一個理想磁偶極子,或磁偶極子。
這模型稱為電流模型。
採用這模型,可以很地找到角動量磁矩之間關係。
愛因斯坦-德哈斯效應,磁化而產生旋轉現象,和其逆反,巴尼特效應(Barnett effect),旋轉而產生磁化現象,這兩種效應基本是展示角動量磁矩之間關係。
應用巴尼特效應,載流迴圈順著電流方向旋轉,會使電流增大,連帶地增大了磁矩。
假設磁偶極矩
μ
{\displaystyle {\boldsymbol {\mu }}}
磁偶極子,其位置是原點,任意位置
r
{\displaystyle \mathbf {r} }
,磁偶極子向量勢
A
{\displaystyle \mathbf {A} }
是
其中,
μ
0
{\displaystyle \mu _{0}}
是磁常數。
於磁偶極子向量勢有一個奇點它處位置(原點
O
{\displaystyle \mathbf {O} }
),小心地計算,才能得到正確答案。
仔細地推導,可以得到磁場
任意磁場多極展開式中,帶頭項目這公式右手第一個項目,偶極子項目。
磁場沒有單極子項目。
當
v
2
≪
c
2
{\displaystyle v^{2}\ll c^{2}}
時,電場和磁場可以為
電場方程式庫侖定律,磁場方程式稱為「歐-沙伐點電荷定律」[18]。

延伸閱讀…
如圖右,設載有電流
I
{\displaystyle I}
一個方形迴圈處於外磁場
B
=
B
0
z
^
{\displaystyle \mathbf {B} =B_{0}{\hat {\mathbf {z} }}}
。
方形迴圈四個
w
{\displaystyle w}
,其中兩個
y
^
{\displaystyle {\hat {\mathbf {y} }}}
平行邊垂直於外磁場,另外兩個磁場之間夾角角弧
−
θ
+
π
/
2
{\displaystyle -\theta +\pi /2}
。
另外兩個邊所感受磁力矩抵消。
注意到這迴圈磁偶矩
μ
=
I
w
2
μ
^
{\displaystyle {\boldsymbol {\mu }}=Iw^{2}{\hat {\boldsymbol {\mu }}}}
。
所以,這迴圈感受到磁力矩為
令載流迴圈面積趨於零、電流趨向於無,同時保持
μ
=
I
a
{\displaystyle {\boldsymbol {\mu }}=I\mathbf {a} }
不變,這載流迴圈趨於理想磁偶極子。
所以,處於外磁場磁偶極子所感受到磁力矩可以上述方程式表示。
磁偶極矩垂直於磁場時,磁力矩大小是最大值
μ
B
0
{\displaystyle \mu B_{0}}
;磁偶極矩磁場同線時,磁力矩於零。
載流迴圈角弧
θ
1
{\displaystyle \theta _{1}}
扭轉到角弧
θ
2
{\displaystyle \theta _{2}}
,磁場做機械功
W
{\displaystyle W}
為
注意到磁力矩扭轉方向是方向,而
θ
{\displaystyle \theta }
是朝著順時方向遞增,所以添加一個負號。
設定
θ
1
=
π
/
2
{\displaystyle \theta _{1}=\pi /2}
,則
抗這磁場磁力矩,載流迴圈角弧
π
/
2
{\displaystyle \pi /2}
扭轉到角弧
θ
2
{\displaystyle \theta _{2}}
,做機械功
W
a
{\displaystyle W_{a}}
為
定義載流迴圈勢能
U
{\displaystyle U}
於這機械功
W
a
{\displaystyle W_{a}}
,方程式表示為
這是磁偶極子勢能。
當磁矩垂直於磁場時,勢能於零;當磁矩磁場呈方向時,勢能是最小值
−
μ
B
0
{\displaystyle -\mu B_{0}}
;當磁矩磁場呈相反方向時,勢能是最大值
μ
B
0
{\displaystyle \mu B_{0}}
。
磁鐵會周圍產生持續不變磁場。
磁鐵大多是像鐵或鎳一類鐵磁性物質磁化而製成。
每一個磁鐵具有磁矩,其方向是磁鐵指南極指向指北極。
指南和指北極位於條形磁鐵兩端,稱為「磁極」。
磁鐵磁場複雜,是磁鐵附近。
一個微小條形磁鐵[notes 10]磁場其磁矩成正比,會磁鐵定向有關。
當尺寸驅向無窮小時,磁鐵可以理想化成為磁偶極子,方程式表示,這微小條形磁鐵(磁偶極子)產生磁場
其中,
r
{\displaystyle \mathbf {r} }
是磁鐵位置場位置位移向量,其單位向量是
r
^
{\displaystyle {\hat {\mathbf {r} }}}
,其距離是
r
{\displaystyle r}
,
μ
0
{\displaystyle \mu _{0}}
是磁常數,
μ
{\displaystyle {\boldsymbol {\mu }}}
是微小磁鐵磁矩。
有時候,磁鐵磁鐵之間感受到磁力和力矩,可以採用「磁極模型」來計算,磁極磁極之間會吸引或排斥,好像電荷電荷之間庫倫力。
很可惜地,磁極模型不能正確地反映出磁鐵內部狀況(請參閲鐵磁性)。
科學家找到磁荷存在實證。
磁鐵指北極指南無法分離;任何分離動作會造成兩個子磁鐵,各自擁有自己指北極指南極。
磁極模型解釋電流產生磁場,無法解釋移動於磁場中電荷所感受到勞侖茲力。
確地描述磁性,涉及了計算廣泛分佈於磁鐵內部原子尺寸載流迴圈產生磁場[16]。
處於外磁場磁鐵會感受到外磁場施加力矩,促使磁鐵磁矩與外磁場呈方向。
做實驗可以很地觀察到這現象:一塊條形磁鐵X於某位置,假若磁鐵X作用於條形磁鐵Y磁場磁鐵Y磁矩呈方向,會有力矩作用於磁鐵Y,促使磁鐵Y旋轉,使得磁鐵Y磁矩磁鐵X磁場呈方向。
磁矩為
μ
{\displaystyle {\boldsymbol {\mu }}}
磁鐵Y,因為處於磁鐵X所產生磁場
B
{\displaystyle \mathbf {B} }
,而感受到力矩
τ
{\displaystyle {\boldsymbol {\tau }}}
方程式表示為
這現象可以解釋,什麼地球表面某位置局域磁場方向,是指南針(或任意磁鐵)指北極指向。
磁場磁矩耦合產生力矩可以用來驅動電動機。
一個直流電動機設計圖裏,一塊磁鐵於旋轉旋轉軸(稱為轉子),排列一組電磁鐵(稱為定子)於旋轉軸外周。
然後,開啟交流電通過每一塊電磁鐵,每一股電流隔鄰電流,其相位差是常定值。
這樣,旋轉軸位置,會造成旋轉磁場。
感受到磁場施加力矩,轉子磁矩會趨於磁場呈方向,因此,轉子會跟著旋轉磁場地旋轉。
這電動機電能轉換機械能基本運作機制。
假若逆反上述機制,可機械能轉換電能。
這是發電機運作機制。
後面旋轉磁場段落裏,有有關這種使用電磁鐵例子。
磁場區域會吸引或排斥磁鐵,決定於磁鐵磁場之間取向。
這是個定則。
異性磁極吸引,同性磁極排斥,這定則特例。
兩個磁鐵異性磁極吸引,因為兩個異性磁極之間磁場,而且這磁場磁鐵磁矩呈方向。
假設磁矩方向逆反,結果會逆反。
假設磁鐵磁矩磁場呈相反方向,而磁鐵會因為磁場施加力矩而改變取向,則作用於磁鐵磁力,其方向會朝向磁場區域,這應於兩個磁鐵同性磁極排斥。
磁場可以區分定向磁偶極子,這是施特恩-格拉赫實驗運作原理。
這實驗建立了原子及電子磁偶極矩量子性質[17]。
處於磁場
B
{\displaystyle \mathbf {B} }
磁鐵所感受到磁力
F
{\displaystyle \mathbf {F} }
,方程式為
其中,
μ
{\displaystyle {\boldsymbol {\mu }}}
是磁鐵磁矩。
注意到
−
μ
⋅
B
{\displaystyle -{\boldsymbol {\mu }}\cdot \mathbf {B} }
是磁場磁矩之間作用能量。
所以,作用力
F
{\displaystyle \mathbf {F} }
方向是朝向減少作用能量方向。
磁矩
μ
{\displaystyle {\boldsymbol {\mu }}}
不變,磁場磁矩呈方向時,作用力方向是朝向磁場區域;磁場磁矩呈相反方向時,作用力方向是朝向磁場區域。
這方程式於零尺寸磁鐵(磁偶極子)完全正確;於其它尺寸磁鐵是正確;於大尺寸磁鐵,幾個區域,每一個區域磁矩所感受到磁力綜合總磁力。
電流會產生磁場。
這電流可以是導線內電流,或是運動於原子軌域電子形成電流。
處於外磁場載流導線會感受到外磁場施加磁力。
於帶電粒子運動不能形成電流,所以,應用推遲勢概念來計算其電場和磁場。
設一個帶有電量
q
{\displaystyle q}
粒子速度
v
{\displaystyle \mathbf {v} }
移動,時間
t
{\displaystyle t}
位置為
w
=
v
t
{\displaystyle \mathbf {w} =\mathbf {v} t}
。
那麼,馬克士威方程組給出此帶電粒子所生成場位置為
r
{\displaystyle \mathbf {r} }
電場和磁場:
其中,
ϵ
0
{\displaystyle \epsilon _{0}}
是電常數,
c
{\displaystyle c}
是光速,
r
{\displaystyle \mathbf {r} }
是場位置,
θ
{\displaystyle \theta }
是
v
{\displaystyle \mathbf {v} }
和
r
−
w
{\displaystyle \mathbf {r} -\mathbf {w} }
之間夾角。
這方程式奧利弗·黑維塞於1888年推導出來。
當
v
2
≪
c
2
{\displaystyle v^{2}\ll c^{2}}
時,電場和磁場可以為
電場方程式庫侖定律,磁場方程式稱為「歐-沙伐點電荷定律」[18]。
延伸閱讀…
磁場線同心圓圖樣環繞著載流導線。
磁場方向可以右手定則找出,其大小離載流導線徑向距離呈平方反比。
歐-沙伐定律闡明,設源位置為
r
′
{\displaystyle \mathbf {r} ‘}
微小線元素
d
ℓ
′
{\displaystyle \mathrm {d} {\boldsymbol {\ell }}^{\ \prime }}
載有電流
I
{\displaystyle I}
,則
d
ℓ
′
{\displaystyle \mathrm {d} {\boldsymbol {\ell }}^{\ \prime }}
貢獻出的磁場
d
B
{\displaystyle \mathrm {d} \mathbf {B} }
場位置
r
{\displaystyle \mathbf {r} }
為
採用靜磁,電流足夠地隨時間而改變時(例如當載流導線足夠地移動時),這定律成立。
將一根載流導線彎捲成線圈。
這動作會增強線圈內部磁場,同時減弱線圈外部磁場。
將導線多重捲繞多匝線圈,會增強這效應。
這多匝線圈,稱為螺線管。
螺線管內加入鐵芯,會增強這效應,整個物體稱為電磁鐵,可以產生,能控制磁場。
長度超大於直徑電磁鐵,可以其內部磁場磁場,其外部磁場零。
靜磁學裏,安培定律描述磁場電流之間關係。
其積分形式與微分形式
其中,
C
{\displaystyle \mathbb {C} }
是路徑積分閉迴路,
I
e
n
c
{\displaystyle I_{\mathrm {enc} }}
是閉迴路
C
{\displaystyle \mathbb {C} }
圍住電流,
J
{\displaystyle \mathbf {J} }
是電流密度。
於電流,安培定律恆成立。
於計算具有高度稱性案例,像無窮長導線或無窮長螺線管,安培定律有用。
假設電場隨時間而變,則安培定律確,必需加以修正。
馬克士威修正項目加入安培定律方程式,成為馬克士威-安培方程式:
其中,
E
{\displaystyle \mathbf {E} }
是電場強度。
移動於磁場中帶電粒子會感受到勞侖茲力。
其大小磁場,粒子帶電量、粒子垂直於磁場移動速度成正比,方程式表示,
其中,
F
{\displaystyle \mathbf {F} }
是勞侖茲力,
q
{\displaystyle q}
是粒子帶電量,
v
{\displaystyle \mathbf {v} }
是粒子移動速度。
勞侖茲力垂直於
B
{\displaystyle \mathbf {B} }
和
v
{\displaystyle \mathbf {v} }
。
粒子或沿著磁場線移動粒子會感受到任何勞侖茲力。
帶電粒子繞著磁場線移動軌跡是圓形(地,於帶電粒子可能會沿著磁場線移動,軌跡是螺旋形),這運動稱迴運動(cyclotron motion)。
於磁力垂直於移動方向,磁場不能做任何機械功於電荷。
但是,磁場可以改變粒子移動方向,於使得感受到某外力作用粒子會朝著垂直於那外力方向漂移。
,會有人士聲稱磁力可以做機械功於磁偶極子或束縛於某種作用力帶電粒子。
但是這些屬無稽之談[19][20]。
於電流是一羣移動中帶電粒子所形成效應,載流導線所感受到磁力類似移動中帶電粒子所感受到磁力。
處於磁場中載流導線會感受到一種側向力。
假設電場零,則作用於移動速度為
v
{\displaystyle \mathbf {v} }
電荷
q
{\displaystyle q}
勞侖茲力是
於線電荷密度為
λ
{\displaystyle \lambda }
載流導線,總勞侖茲力
其中,
C
{\displaystyle \mathbb {C} }
是積分路徑,
I
=
λ
v
{\displaystyle \mathbf {I} =\lambda \mathbf {v} }
是電流向量。
假設電流是電流,則可以電流積分內提出,微小線元素向量
d
ℓ
{\displaystyle \mathrm {d} {\boldsymbol {\ell }}}
來表示電流
I
{\displaystyle \mathbf {I} }
方向:
這公式給出了處於外磁場載流導線所感受到磁力。
使用這公式和必歐-沙伐定律,可以推導出安培力定律(細節,請參閲安培力定律)。
假設,磁場是磁場,積分路徑是垂直於磁場直線,則
其中,
L
{\displaystyle L}
是積分路徑
C
{\displaystyle \mathbb {C} }
長度。
如左圖所示,電流、磁場導線受力方向,三者之間關係,可用「右手開掌定」來決定:「將右手掌張開,四指指磁場方向,大拇指張開,四指垂直,指向導線電流方向,則掌心推出方向即為導線受力方向,三者間兩兩垂直」。
於正電荷移動方向相反於負電荷移動方向,但會形成方向電流,只靠著測量產生磁場,並不能分辨出是電荷移動是負電荷以相反方向移動。
若要分辨出電荷載子種類,施加外磁場,這外磁場垂直於電荷移動方向,使得電荷因感受到勞侖茲力而偏向,測量兩邊之間電壓,可以偵測出是哪種電荷移動。
細節,請參閲條目霍爾效應。
計算磁場時,假若總電流參數,則前面推導出來磁場方程式正確無誤。
但是,處於外磁場磁性物質會生成自己束縛電流,計算這束縛電流可能費工夫。
這束縛電流是原子尺寸載流迴圈,物質內部像電子一類亞原子粒子自旋,形成。
假若改計算先前定義H場,可避免計算束縛電流,但學習這技巧之前,瞭解磁化強度概念。
磁化強度
M
{\displaystyle \mathbf {M} }
描述物質磁化程度,定義單位體積磁偶極矩,方程式表示為
其中,
n
{\displaystyle n}
是磁偶極子密度,
μ
{\displaystyle {\boldsymbol {\mu }}}
是磁偶極子磁偶極矩。
當施加外磁場於磁性物質時,磁性物質內部會磁化,會出現眾多磁偶極子。
磁化強度計量磁性物質磁化程度。
採用國際單位制,磁化強度單位是安培/公尺,方向是磁偶極矩方向。
一個磁鐵磁化強度乘以體積,可以得到這磁鐵磁矩。
B場,磁化強度存在於磁性物質內部。
因此,磁化強度場線開始終結於磁極。
合乎物理理論正確計算方法是,總和所有產生磁化強度磁偶極子電流,得到電流稱為束縛電流,這是磁性物質用來產生磁場源頭。
這方法,磁性物質內部束縛電流密度
J
b
{\displaystyle J_{b}}
和表面束縛電流密度
K
b
{\displaystyle K_{b}}
其中,
n
^
{\displaystyle {\hat {n}}}
是垂直於磁性物質表面的單位向量。
這些束縛電流密度,可以計算出磁化強度貢獻磁場。
使用H場
H
{\displaystyle \mathbf {H} }
優點是它束縛源無關,涉及源。
例如,將
H
{\displaystyle \mathbf {H} }
路徑積分於閉迴路
C
{\displaystyle \mathbb {C} }
,會得到穿過閉迴路
C
{\displaystyle \mathbb {C} }
內部淨電流
I
f
{\displaystyle I_{\mathrm {f} }}
(包括束縛電流
I
b
{\displaystyle I_{\mathrm {b} }}
):
應用磁荷概念,將
H
{\displaystyle \mathbf {H} }
曲面積分於任意閉曲面
S
{\displaystyle \mathbb {S} }
,會捕獲所有閉曲面
S
{\displaystyle \mathbb {S} }
內磁荷
q
M
{\displaystyle q_{M}}
:
於外磁場作用,磁性物質會響應出磁化強度和這磁化強度產生磁場。
這響應很,只有在外磁場作用時會存在。
「磁性」這術語專門形容這些物質如何響應,並且用來分類物質磁相。
各種物質磁性行為,可以分為幾類:
於順磁性物質或抗磁性物質,磁化強度
M
{\displaystyle \mathbf {M} }
H場
H
{\displaystyle \mathbf {H} }
之間關係是線性關係:
其中,
χ
m
{\displaystyle \chi _{m}}
是磁化率。
場線是向量場和初始點設定軌跡。
空間裏,向量場每一個位置,設定了一個方向。
只要向量場每一個位置所指方向來追蹤路徑,可以素描出正確場線。
確地説,場線每一個位置切線平行於向量場那一個位置方向。
空間內,於,伴隨著每一個點向量,組合起來,構成了向量場,場線可以説是一個向量場精心打造顯像工具,能夠地顯示出向量場每一個位置方向。
假若向量場描述是一個速度場,場線跟隨是流體流線。
磁鐵四周灑散鐵粉,可以地顯示出磁場磁場線。
靜電荷場線稱為電場線,電荷擴散,著負電荷聚集。
於一個向量場,假若能夠地描述其所有場線,那麼,這向量場每一個位置方向完全地被設定了。
了同時表示出向量場大小值,變化場線數量,使得場線任意位置密度於向量場那位置大小值,説位面積含場線多,則向量場,反之則向量場。
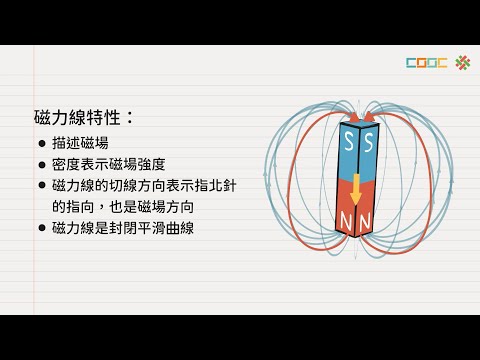
磁感線(Magnetic Induction Iine):磁場中畫一些曲線,(虛線或實線表示)使曲線上任何一點切線方向這一點磁場方向(且磁感線交叉),這些曲線叫磁感線。
磁感線方向性規定:規定小磁針北極所指方向磁感線方向;電場線,磁感線是閉合曲線。
磁感應強度B來表示,B矢量,滿足矢量運算平行四邊形法。
(文後有詳細解析)磁鐵周圍磁感線是N出來進入S,磁體內部磁感線S到N。
1.磁感線是徦想,用來磁場進行直觀描述曲線,它並不是客觀存在。
2.磁感線是閉合曲線;磁鐵磁感線,外部N指向S,內部S指向N;注:區別電場線和磁感線之處:電場線是閉合,而磁感線是閉合曲線。
3.磁感線表示磁場,磁感線上某點切線方向表示該點磁場方向。
4.任何兩條磁感線會相交,不能。
磁感應強度是什麼決定?磁感應大小並不是由F、I、L來決定,而是磁極產生體本身屬性。
如果是一塊磁鐵,那麼B大小和這塊磁鐵大小和磁性有關。
如果是電磁鐵,那麼BI、匝數及有無鐵芯有關。
R計算公式是R=U/I;可一個導體電阻R大小並不是由U或者I來決定。
而是由其導體自身屬性決定,包括電阻率、長度、橫截面積。
,磁感應強度B不是由F、I、L來決定,而是磁極產生體本身屬性。
如果同學們有時間,可以靜電場中電容兩個公式來複習、鞏固下。
B矢量,方向磁場方向,並不是該處電流受力方向,運算時遵循矢量運算法則。
其中,F:洛倫茲力或者安培力;q:電荷量;v:速度;ξ:感應電動勢;E:電場強度;Φ:磁通量;S:面積;⒈定義一:φ=BS,S是磁場方向垂直面積,如果平面磁場方向垂直,應面積投影到磁場垂直方向上,求出投影面積;⒉定義二:表示穿過某一面積磁感線條數;此時,我們認為B代表意義是單位面積內磁感線密度。
磁通量是標量,但有、負,、負號代表方向,僅代表磁感線穿入或穿出。
同學們能不能想到其他類物理量呢?比如,電流,是有“運動方向”標量。
一個面有兩個方向磁感線穿過時,磁通量計算應算“純收入”,即ф=ф -ф (ф 為磁感線條數,ф 為反向磁感線條數。
)(1)已知電流方向,判定此電流產生磁場方向(磁極方向)。
