在測繪工作中,方位角是最基本的方位元素,也是導航定位和航空飛行等領域的重要元素。所謂方位角,是指從北開始的順時針旋轉角度,指示了目標相對於真北的方位。具體來説,我們可以將方位角分為真方位角和磁方位角兩種。真方位角以地球的真北方向為基準,而磁方位角則是以地球的磁北極方向為基準。
磁方位角是測繪工作中重要的概念之一,磁方位角的計算方法有多種,最常用的是迭代法和正算法。迭代法通過多次計算得到目標相對於真北的角度,而正算法則是直接計算出目標相對於真北的方向。在實際測量中,我們通常使用磁羅盤測量得到的磁方位角。AA為起點到終點的方位角,起點和終點為相應座標的數值。


修改後的文章
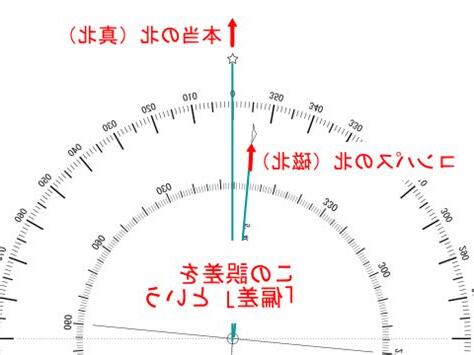
在測繪工作中,方位角是最基本的方位元素,也是導航定位和航空飛行等領域的重要元素。所謂方位角,是指從北開始的順時針旋轉角度,指示了目標相對於真北的方位。具體來説,我們可以將方位角分為真方位角和磁方位角兩種。真方位角以地球的真北方向為基準,而磁方位角則是以地球的磁北極方向為基準。在實際測量中,我們通常使用磁羅盤測量得到的磁方位角。方位角的計算方法有多種,最常用的是迭代法和正算法。迭代法通過多次計算得到目標相對於真北的角度,而正算法則是直接計算出目標相對於真北的方向。下面我們就來介紹一下計算方法。其中,AA為起點到終點的方位角,起點和終點為相應座標的數值。請注意,AA的值可能會受到所使用的座標系的影響。## 迭代法迭代法是一種比較常用的計算方位角的方法,它的基本思想是將目標點的座標和起點的座標代入以下公式:\[ \theta = \arccos \left( \frac{ \sin (y_2 – y_1) \sin (x_2 – x_1) } { \sqrt{ \sin^2 (y_2 – y_1) + \cos^2 (y_1) } \sqrt{ \sin^2 (x_2 – x_1) + \cos^2 (x_1) } \right) \]其中,\( \theta \)表示角度,\( y_2 \)和\( y_1 \)分別表示目標點和起點的緯度,\( x_2 \)和\( x_1 \)則表示目標點和起點的經度。通過多次迭代計算,即可得到目標點相對於起點的方位角。## 正算法正算法是一種直接計算目標點相對於真北方向的計算方法,它主要藉助了三角函數的知識。假設目標點和起點的座標均已知,我們可以使用以下公式進行計算:\[ \text{方位角} = \arctan \left( \frac{ \sin (y_2) \sin (y_1) – \cos (y_2) \cos (y_1) \cos (x_2 – x_1) } { \sin (x_2 – x_1) } \right) + \pi \]請注意,上述計算中使用的\( \arccos \)和\( \arctan \)函數都是有兩種可能的值的,因此在實際應用中,可能需要根據具體情況添加條件以確定方向是正向還是逆向。總之,通過上述方法,我們可以準確地計算出目標點相對於起點的方位角。
磁方位
磁方位是指物體相對於地球磁場的方向。地球擁有自己的磁場,它是由地球核心內部的電流產生的,並在地球周圍形成一個磁場。
在導航和定位中是一個非常重要的概念。許多動物和甚至是一些人類都具有感知和利用地球磁場的能力,這允許它們導航和找到自己的方向。
在現代科技中,我們也利用磁方位以各種方式,例如指南針,GPS和地磁儀。指南針是一種簡單的裝置,其中包含一個指針,指示出地球磁場的方向。它被廣泛應用於航海,飛行,房屋建造和個人使用中。
GPS定位系統也利用了地球的磁場信息。透過衞星信號和接收器,GPS能夠計算出接收器相對於地球的磁方位,從而準確地定位位置。
地磁儀是一種更高精度的儀器,用於測量地球磁場的強度和方向。這些數據在地球科學研究,磁學研究和地震監測中起著關鍵作用。
磁方位的概念還在航空和太空探索中發揮著重要作用。導航和定位對於飛行器和航天器來説至關重要,需要準確地知道它們相對於地球的位置和方向。
總而言之,磁方位在現代社會中扮演著重要的角色。無論是個人導航,定位系統,還是科學研究和探索,我們都依賴於磁方位來尋找方向。
延伸閲讀…
磁方位角定義| GIS 字典
磁方位角- 抖音百科
