在粒子物理學中,費米子與玻色子是兩類基本的粒子,它們之間存在著深刻的差別。費米子如電子、夸克等,遵循費米—狄拉克統計法,具有半整數自旋,且在同一量子狀態下只能存在有限個數。玻色子如光子、引力子等,遵循玻色—愛因斯坦統計法,具有整數自旋,且在同一量子狀態下可以存在任意個數。因此,費米子與玻色子的性質和行為在不同條件下可能會產生顯著的差異。
- 組成物質的能力: 費米子是構成物質的基本粒子,而玻色子則負責粒子之間的相互作用。
- 統計法: 費米子遵循費米-狄拉克統計法,玻色子遵循玻色統計法。
費米子與玻色子的構成與性質
在物質的構成中,費米子扮演著基本粒子的角色,如電子、質子、中子等。這些費米子是構成我們宇宙這個「巨大建築」的基本材料。而玻色子則負責在不同費米子之間傳遞各種相互作用,就像是將不同材料粘合在一起的「基本方法」。
費米子受泡利不相容原理的約束,這使得研究費米子多粒子系統變得更加複雜。相較之下,玻色子多粒子系統的研究方法則簡單得多,因為玻色子沒有不相容原理的限制。


不同層次的組裝需要不同的相互作用,這些相互作用正是由玻色子如光子、膠子、W粒子等的傳遞所實現的。
從性質上來看,費米子具有半分數自旋,而玻色子則為整數自旋。這使得玻色子更容易被描述為一個場,而費米子則需要使用波函數來表示。
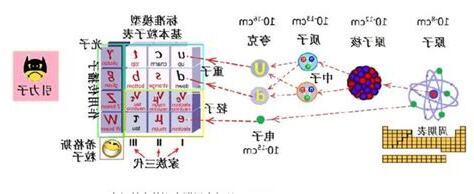
在描述粒子運動方面,費米子使用狄拉克方程,而玻色子則使用克利格-哥德爾(Klein-Gordon)方程。這些方程是由不同的作用量經由求變分得到的。
費米子受泡利不相容原理的約束,這使得研究費米子多粒子系統變得更加複雜。相較之下,玻色子多粒子系統的研究方法則簡單得多,因為玻色子沒有不相容原理的限制。
在凝聚態物理理論中,費米子與玻色子多粒子系統的研究方法存在顯著差異。
全同粒子
對於全同粒子,當考慮 n 個粒子的置換粘合時,我們研究的是空間中路徑的分類,即基本羣,並尋找其一維酉表示。在量子力學中,全同粒子是一類無法區分的粒子。這類粒子包括基本粒子,如電子、光子,以及合成的粒子,如原子和分子。
粒子區分的兩種方法
- 第一種方法是基於粒子所具有的不同物理性質,如電荷、質量、自旋等。如果粒子的性質不同,就可以通過測量這些差異來區分它們。但事實上,同類粒子被發現具有完全相同的物理性質,例如,所有電子的電荷都是相同的。這就是為何常説「電子的電荷」,而不是特定電子的電荷。
- 第二種方法是根據粒子的軌道來區分。然而,這種方法與量子力學的基本原理相矛盾。根據量子理論,粒子的位置是由波函數決定的,並且只能在給定位置給出機率。隨著時間的推移,波函數會擴散,導致粒子之間的波函數重疊。一旦發生重疊,就無法根據位置來區分兩個粒子。因此,粒子變得越來越難以區分。
量子力學的數學表述
為了具體説明,我們假設有一個含有兩個全同粒子的量子系統。由於這些粒子具有相同的物理性質,它們的態向量的希爾伯特空間是相同的。如果一個粒子的希爾伯特空間被標記為 H,則兩個粒子的整體希爾伯特空間是張量積 H ⊗ H。

設 n 為單獨粒子量子態的(離散)量子數(
結合系統的量子態
當一個粒子處於量子態
|n_{1}\rangle,另一個粒子處於量子態|n_{2}\rangle時,結合系統的量子態可能是以下的形式:在檢視多粒子量子態時,交換對稱性是一個關鍵概念。當我們考慮n個粒子的量子系統時,我們可以定義一個交換算符Pij,它會將第i個粒子的量子態與第j個粒子的量子態交換。這些算符會遵守一定的交換規則,這些規則決定了量子態的總體對稱性。例如,如果Pij與Pjk互換時 sign(i-j)(j-k),則表明量子態具有全對稱性或全反對稱性,這取決於n個粒子是 Bosons 還是 Fermions。


延伸閲讀…
費米子和玻色子有什麼區別?
全同粒子- 維基百科,自由的百科全書
對稱態與反對稱態
對於全同粒子,量子態的表達式可能是:
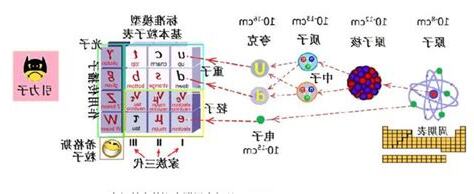
S\{n_{1}, n_{2}\}A\{n_{1}, n_{2}\}n_{1} = n_{2}1\sqrt{2}\{\frac{|n_{1}, n_{1}\rangle + |n_{2}, n_{2}\rangle}{\sqrt{2}}0n_{1} \neq n_{2}\{\frac{|n_{1}, n_{2}\rangle + |n_{2}, n_{1}\rangle}{\sqrt{2}}改寫後的文章
在量子力學中,我們關注粒子量子態的特殊對稱性,稱為交換對稱性。這對稱性與線性算符P相關,稱為交換算符。當P作用於含有兩個粒子的量子系統時,它會交換兩個粒子的量子態。原來粒子1的量子態為|ψ⟩,粒子2的量子態為|ϕ⟩。經P作用後,粒子1的量子態變為|ϕ⟩,而粒子2的量子態變為|ψ⟩。P是厄米算符和麼正算符,可以用來描述粒子量子態交換的對稱性。P的平方等於單位算符,即P2 = 1。因此,P的本徵值為+1或-1,對應的本徵態是對稱態和反對稱態。我們可以觀察到,經過粒子的交換,對稱態與反對稱態只是被乘以+1或-1的因子,而不是在希伯爾特空間內旋轉。
在檢視多粒子量子態時,交換對稱性是一個關鍵概念。當我們考慮n個粒子的量子系統時,我們可以定義一個交換算符Pij,它會將第i個粒子的量子態與第j個粒子的量子態交換。這些算符會遵守一定的交換規則,這些規則決定了量子態的總體對稱性。例如,如果Pij與Pjk互換時 sign(i-j)(j-k),則表明量子態具有全對稱性或全反對稱性,這取決於n個粒子是 Bosons 還是 Fermions。
延伸閲讀…
量子,玻色子,費米子,讓你看懂各種粒子的區別
你是費米子?還是玻色子?
粒子的全同與量子態的對稱性
這證明粒子標籤無物理意義,與不可區分性相符。由於P是厄米算符,因此它可被測量,且粒子的全同性意味著哈密頓量可以寫成對稱形式。
粒子的種類決定其量子態的對稱性。例如,光子和氦-4原子為對稱態,而電子、質子為反對稱態。
對稱態的粒子稱為玻色子,它們遵循玻色-愛因斯坦統計。反對稱態的粒子稱為費米子,它們遵循費米-狄拉克統計。在某些二維系統中,可能有混合對稱性的任意子,它們遵守分數統計。
自旋統計理論將全同粒子的交換對稱性追溯至它們的自旋。這理論表明玻色子的自旋是正整數,費米子的自旋是半整數,任意子的自旋是分數。
改寫後的文章
在一個量子力學的系統中,我們有若干個具有不同量子數的粒子,這些粒子的量子態可以用一系列的量子數來描述。設有N個量子數,分別為n1、n2、…、nN,每個量子數對應一個特定的粒子狀態。在這個系統中,我們關注其中特定的量子數η1、η2、…、ηL,它們分別出現了N1、N2、…、NL次。當我們考慮這些粒子為玻色子時,描述這些粒子的量子態滿足完全對稱性,即對於任何兩個粒子的交換,系統的狀態都是不變的。這意味著在多粒子態中,所有的粒子都是完全相同的,沒有任何個體差別。
