互補角與鄰角
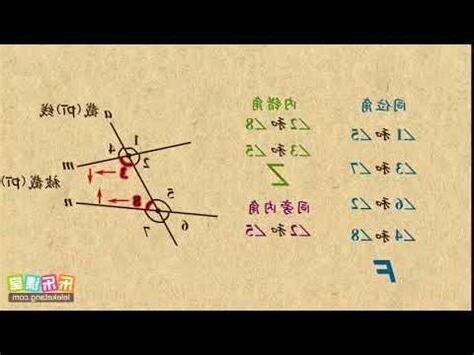
在平面幾何中,鄰角指的是一對共同擁有頂點和一條公共邊的角,且兩者的其他兩邊位於公共邊的不同側。兩個角被稱為鄰補角,當它們是由兩條相交直線所形成的,共用一個頂點,且一方的邊是另一方的反向延長線。


每個角有兩個鄰補角,且這些角平分線互相垂直。一個角與其鄰補角的和等於 180 度。
互補角則是指兩個角的和等於 180 度。兩個角稱為互補角,其度數之和等於一個平角。
| 種類 | 定義 | 角度和 |
|---|---|---|
| 鄰角 | 共用頂點和公共邊的角 | 兩角之和不等於 180 度 |
| 鄰補角 | 共用頂點和一條公共邊的兩個角 | 兩角之和等於 180 度 |
| 互補角 | 度數之和等於 180 度的兩個角 | 兩個角的和等於 180 度 |
鄰角是什麼?
在幾何學中,鄰角指的是兩條相交直線形成的四個角中的兩組相鄰角。換句話説,鄰角就是共用一個頂點的兩個角。
兩個相鄰角的和等於 180 度。這個性質被稱為 鄰角定理。
table
| 相鄰角 | 角度和 |
|---|---|
| 兩條直線相交的四個角中的兩組角 | 180 度 |
鄰角的種類
鄰角有兩種種類:
-
同側鄰角:兩個相鄰角位於一條直線的同側,也就是説它們都朝向同一方向。同側鄰角之和等於 180 度。
-
異側鄰角:兩個相鄰角位於一條直線的不同側,也就是説它們朝向不同的方向。異側鄰角之和也等於 180 度。
鄰角的應用
鄰角定理在幾何學中有很多應用,例如:
- 計算平行四邊形和菱形的對角線的長度。
- 證明三角形的外角和等於 180 度。
- 求一個多邊形所有內角的和。
例子
下圖中,∠A 和 ∠B 是相鄰角,∠C 和 ∠D 是相鄰角。
∠A
/ \
/ \
/ \
∠C ∠B
由於 ∠A 和 ∠B 是同側鄰角,因此它們的和為 180 度:
∠A + ∠B = 180 度
由於 ∠C 和 ∠D 是異側鄰角,因此它們的和也為 180 度:
