在資訊科學中,「2-3樹」是一種在數據結構中常用的自平衡二叉搜索樹。它是一種有效率的方法,用於儲存和搜索大量數據,並且即使在數據插入和刪除操作後也能保持平衡的特性。此外,2-3樹在實踐中具有廣泛應用,例如在資料庫中用於提高查詢效率,以及在操作系統的記憶體管理中發揮作用。接下來,我們將深入探討2-3樹的結構、操作和應用。
2-3 樹的結構
- 節點結構: 2-3 樹的每個節點可以包含 0、1、2 或 3 個鍵值對。如果一個節點包含 1 個鍵值對,它稱為 1-節點;如果包含 2 個鍵值對,它稱為 2-節點;如果包含 3 個鍵值對,它稱為 3-節點;如果一個節點沒有鍵值對,它稱為空節點。
- 搜索(尋找)操作: 在 2-3 樹中查找一個特定的鍵值對和在二叉搜索樹中類似,可以通過比較鍵值對和路徑上的節點鍵值對來實現。
- 插入操作: 插入一個新鍵值對首先在一棵相對平衡的 2-3 樹中進行,如果要在 1-節點或 2-節點中插入,可能需要將這個節點和它的父節點合併。
- 刪除操作: 刪除一個鍵值對可能會導致不平衡的樹,因此在刪除後需要進行調整,以保持樹的平衡。
2-3 樹的特點與優勢
- 高度平衡: 2-3 樹能夠自動保持高度的平衡
2-3-4 樹是一種自平衡的搜索樹,它在計算機科學中應用廣泛。它們被設計用來保持數據的有序性,並且可以在 時間內進行搜索、插入和刪除操作。2-3-4 樹的節點結構使得它們具有強大的平衡性,這有助於保持樹的高度最小化,進而提高數據訪問的速度。
改寫後的文章
簡介
在數據結構中,二叉搜索樹(BST)是一種常用的樹形結構,其中每個節點最多有兩棵子樹,且左子樹的所有節點都小於或等於根節點的值,右子樹的所有節點都大於根節點的值。然而,當 BST 中的操作頻繁,尤其是隨機數據的插入和刪除時,樹的形狀可能會變得極其不平衡,從而影響數據訪問的效率。為了維持樹的平衡性,人們設計了多種自我平衡的二叉搜索樹,其中最著名的是紅黑樹(Red-Black Tree)。紅黑樹通過聰明的着色策略和樹結構的調整,可以保證在任何時候樹的深度都約等於樹中節點數目的對數。
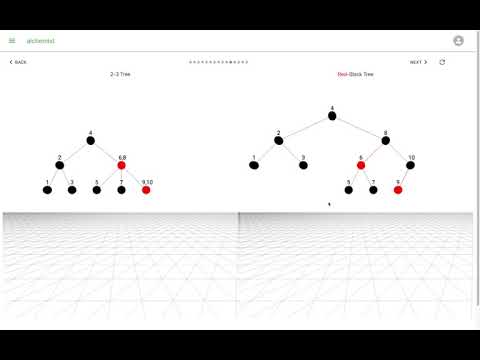

- 在 2-3-4 樹中,插入操作首先在葉節點層面進行,形成一個暫時的 5 節點。然後,根據樹的結構和插入的值的位置,進行一系列的上溢調整以保持平衡。這可能涉及將數據元素從一個節點移到另一個節點,或者通過旋轉操作來重新排列節點的子節點。
刪除操作
刪除操作在 2-3-4 樹中可能會導致下溢,即葉節點可能會因為刪除操作而變成空的。為了避免這種情況,在刪除之前,樹會進行一系列的調整。這些調整可能包括從兄弟節點借出數據元素,或者進行樹節點的旋轉。
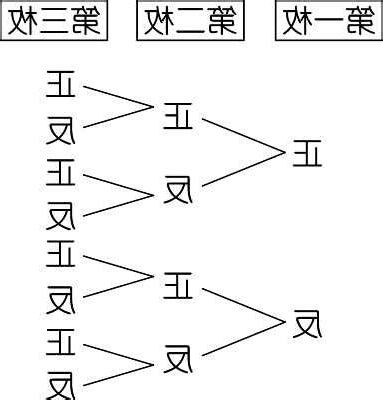
改寫後的文章
簡介
在數據結構中,二叉搜索樹(BST)是一種常用的樹形結構,其中每個節點最多有兩棵子樹,且左子樹的所有節點都小於或等於根節點的值,右子樹的所有節點都大於根節點的值。然而,當 BST 中的操作頻繁,尤其是隨機數據的插入和刪除時,樹的形狀可能會變得極其不平衡,從而影響數據訪問的效率。為了維持樹的平衡性,人們設計了多種自我平衡的二叉搜索樹,其中最著名的是紅黑樹(Red-Black Tree)。紅黑樹通過聰明的着色策略和樹結構的調整,可以保證在任何時候樹的深度都約等於樹中節點數目的對數。
插入操作
基本操作
在紅黑樹中插入一個新節點的基本操作相對簡單。我們只需要將新節點設為紅色,並將其插入到恰當的位置。如果插入後的樹打破了紅黑樹的性質,我們需要通過一系列的調整操作來修復它。

Case 1
當要刪除的節點是單獨的終端節點時,我們只需要將其父節點連向該節點的指針置為空,並將父節點的顏色變為黑色。如果該父節點本身就是黑色,則不需要進行任何額外的操作。反之,如果父節點是紅色,則需要將其變為黑色,並且將祖先節點中的所有紅色節點都變為黑色,直到遇到黑色的兄弟節點為止。這樣做的目的是保持從根節點到每個葉節點的黑色節點的數目不變。


延伸閲讀…
原始樹結構 插入後的樹結構 < 對於紅黑樹的刪除操作,我們可以根據要刪除的節點在樹中的不同位置,將其分為四種情況:1. 單獨的終端節點(葉節點或單子節點)被刪除;2. 位於樹最下層的節點被刪除;3. 位於樹中層的節點被刪除;4. 中層節點的兄弟節點也是黑節點的刪除。

Case 1
當要刪除的節點是單獨的終端節點時,我們只需要將其父節點連向該節點的指針置為空,並將父節點的顏色變為黑色。如果該父節點本身就是黑色,則不需要進行任何額外的操作。反之,如果父節點是紅色,則需要將其變為黑色,並且將祖先節點中的所有紅色節點都變為黑色,直到遇到黑色的兄弟節點為止。這樣做的目的是保持從根節點到每個葉節點的黑色節點的數目不變。
延伸閲讀…
Case 2
當要刪除的節點位於樹的最下層且具有兩個子節點時,我們將其作為 Case 3 來處理。
Case 3
當要刪除的節點位於樹的中層且具有兩個子節點時,我們可以先找出它的後繼節點(即在樹中具有比該節點大或相等的值的最小節點), 並將該後繼節點的值傳遞給要刪除的節點,然後刪除後繼節點。因為後繼節點有可能是黑的,所以在刪除後繼節點時,可能需要進行Case 1的操作。如果後繼節點是黑色的,且它的兄弟節點也是黑色的,則需要對它的兄弟節點
