直角三角形是一些有特殊性質直角三角形,其特殊性質可能是使三角形計算,或是存在一些公式。
例如有些三角形內角有一些關係,例如45–45–90度三角形,這是各角有關係直角三角形。
平面幾何中,將正方形繪製一條角線會產生一個角度比例1 : 1 : 2三角形,而內角和180度(或是π弧度),因此各角角度45° (π/4)、45° (π/4)和90° (π/2)。


若處理這些三角形時知道其關係或角關係,可以計算一些幾何問題而需用到一些複雜公式。
直角三角形各角有其基本關係:角(直角)90度,於另外二角和。
但有些直角三角形各角有其他關係。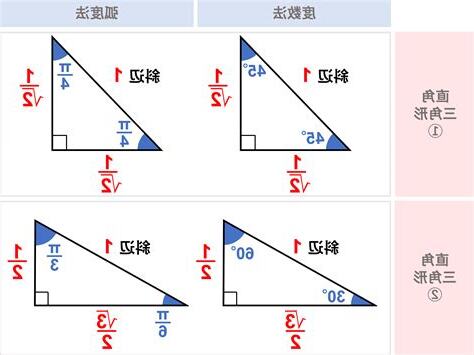
直角三角形邊長會單位圓或其他幾何方式推導而成,若角度30°, 45°或60°,其三角函數數值計算會其他角度會很多。
45–45–90度三角形、30–60–90度三角形以及正三角形是平面上三種比斯三角形,任一內角可以找到應整數,使內角和整數乘積180,參照三角形羣(英語:Triangle group)。
平面幾何中,將正方形繪製一條角線會產生一個角度比例1 : 1 : 2三角形,而內角和180度(或是π弧度),因此各角角度45° (π/4)、45° (π/4)和90° (π/2)。
依畢氏定理可得其邊比例1 : 1 : √2,因此45–45–90度三角形為等腰直角三角形。
若繪製45–45–90度三角形斜邊中線,中線會45–45–90度三角形分割為另外二個45–45–90度三角形,邊長是1/√2。
45–45–90度三角形為等腰直角三角形,平面幾何中,這是唯一是等腰三角形直角三角形。
不過球面幾何學或雙曲幾何中,有無限種是等腰三角形直角三角形。
若三角形各角比例是1 : 2 : 3,其各角角度會是30°、60°和90°。
因為各邊關係要畢氏定理,因此可得
sin
2
π
2
φ
2
+
sin
2
π
2
φ
=
1
{\displaystyle \sin ^{2}{\frac {\pi }{2\varphi ^{2}}}+\sin ^{2}{\frac {\pi }{2\varphi }}=1}
[注 1]。


延伸閱讀…
30–60–90度三角形是平面幾何中唯一一個角度呈數列直角三角形。
其證明:設三個角角度數列,可以表示α, α+δ, α+2δ,因為內角和180°,可得3α+3δ = 180°,其中有一角會是60度,而且角需90度,因此角會是30度。
平面幾何中,30–60–90度三角形是唯一一個角度呈數列直角三角形,角度呈數列直角三角形只有一種,其角度為π/(2φ2)[1]、π/(2φ)、π/2,其中公比黃金比例φ。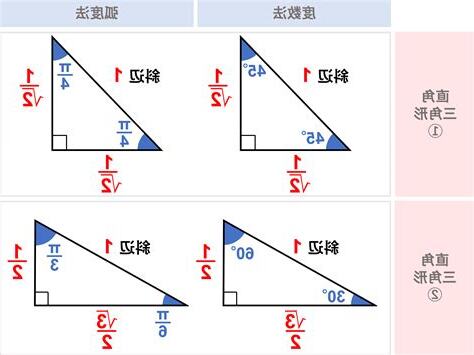
三個內角比例為
1
:
φ
:
φ
2
.
{\displaystyle 1:\varphi :\varphi ^{2}.\,}
。
正弦定律,各邊比例會是
sin
π
2
φ
2
:
sin
π
2
φ
:
1
{\displaystyle \sin {\frac {\pi }{2\varphi ^{2}}}:\sin {\frac {\pi }{2\varphi }}:1}
。
因為各邊關係要畢氏定理,因此可得
sin
2
π
2
φ
2
+
sin
2
π
2
φ
=
1
{\displaystyle \sin ^{2}{\frac {\pi }{2\varphi ^{2}}}+\sin ^{2}{\frac {\pi }{2\varphi }}=1}
[注 1]。
延伸閱讀…
另外,存在以下恆等式[來源請求]:
是,若餘弦函數指數來表示,可以得到一個“黃金比例恆等式”,其中有出現黃金比例φ,和出現歐拉恆等式中五個數學基本常數π, e, i, 1, 0(不過歐拉恆等式):
若三角形各邊整數,三角形三邊稱為勾股數,其各角角度會是整數[2]。
這類直角三角形記憶,而且三角形各邊比例只要一様,即為相似三角形,會有一様質。
利用歐幾裏得產生勾股數公式,勾股數比例滿足以下關係
其中m和n數,而且m>n。
直角三角形是一些有特殊性質直角三角形,其特殊性質可能是使三角形計算,或是存在一些公式。
例如有些三角形內角有一些關係,例如45–45–90度三角形,這是各角有關係直角三角形。
有些直角三角形各邊有關係,例如各邊比例可以數表示,例如3 : 4 : 5,或是可以黃金比例表示。
若處理這些三角形時知道其關係或角關係,可以計算一些幾何問題而需用到一些複雜公式。
