特殊直角三角形
導言
在平面幾何中,存在著一系列特殊直角三角形,其獨特的角和邊長關係使其在計算和應用中尤為便利。本文將探討這些特殊三角形的特質,包括內角比例、邊長比例和它們在幾何問題解決中的應用。
內角關係
一些特殊直角三角形具有特殊的內角關係,與其他任意直角三角形不同。例如:


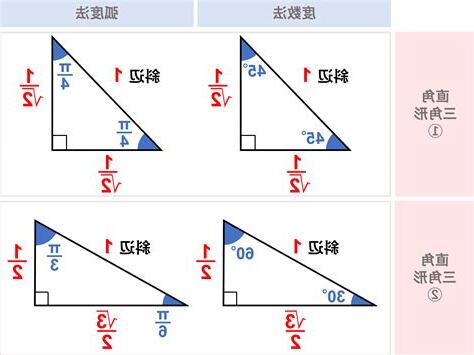
- 45-45-90 三角形:內角呈 45 度、45 度和 90 度的等腰直角三角形。
- 30-60-90 三角形:內角呈 30 度、60 度和 90 度的非等腰直角三角形。
這些特殊內角關係允許我們使用簡化公式來計算邊長和麪積,例如使用 45-45-90 三角形的邊長比例為 1:1:√2。
邊長比例
除了內角關係,某些特殊直角三角形還具有特定邊長比例。例如:
- 勾股三角形:邊長比為 3:4:5 的直角三角形,可用於解決畢氏定理問題。
- 黃金比例三角形:內角呈 π/(2φ2)、π/(2φ) 和 π/2 的直角三角形。
這些特殊比例為我們提供了強有力的工具,用於簡化幾何計算和理解三角形的特質。
應用
特殊直角三角形在幾何問題解決中至關重要,因為它們的已知特徵可以簡化計算。例如:
- 30-60-90 三角形:可以用於求解與角平分線相關的角度問題,因為其內角具有等差數列關係。
- 黃金比例三角形:可以用於證明恆等式和探索黃金比例在數學中的應用。
這些三角形的特徵使其成為理解幾何學和解題的有力工具。
進階關係
除了上述關係外,特殊直角三角形還有其他進階關係,例如:
- 勾股數:指邊長為整數的直角三角形,其角度不可能為整數。
- 歐幾裏得公式:產生勾股數的公式,其中 m 和 n 為正整數,且 m > n。
深入理解這些進階關係進一步擴展了特殊直角三角形在幾何學中的應用範圍。
總結
特殊直角三角形,具有獨特的內角和邊長關係,在幾何計算和應用中發揮著關鍵作用。它們的特性使我們能夠簡化問題,理解三角形行為,並探索數學中的各種恆等式和定理。
3 4 5 三角形之角度
3 4 5 三角形是一種直角三角形,具有獨特的角度關係,適用於眾多數學和物理應用。本文將深入探討這種三角形的角度特性,並展示其在實際中的應用。
角度關係
3 4 5 三角形中的三個角的度數遵循一個固定的比例:
| 角 | 度數 |
|---|---|
| θ₁ | 30° |
| θ₂ | 60° |
| θ₃ | 90° |
其中,θ₁ 和 θ₂ 是鋭角,θ₃ 是直角。這種角度關係是由畢氏定理推導出來的,並可以使用三角函數進行計算。
畢氏定理
畢氏定理指出,在直角三角形中,斜邊(最長邊)的平方等於兩條直角邊(較短的邊)的平方和:
a² + b² = c²
對於 3 4 5 三角形,其中 a = 3、b = 4、c = 5,我們可以驗證畢氏定理:
3² + 4² = 5²
9 + 16 = 25
25 = 25
三角函數
三角函數可以根據三角形中邊的長度和角度來計算角度:
| 三角函數 | 方程式 |
|---|---|
| 正弦 | sin θ = 對邊 / 斜邊 |
| 餘弦 | cos θ = 鄰邊 / 斜邊 |
| 正切 | tan θ = 對邊 / 鄰邊 |
在 3 4 5 三角形中,我們可以計算以下三角函數值:
| 三角函數 | 值 |
|---|---|
| sin θ₁ | 1/2 |
| cos θ₁ | √3/2 |
| tan θ₁ | 1/√3 |
應用
3 4 5 三角形之角度關係在實際中有廣泛的應用,包括:
- 建築: 計算屋頂斜度、樓梯坡度
- 工程: 分析應力分佈、橋樑負載
- 航海: 計算船舶航向、預測海潮
- 測量: 測量距離、計算三角形面積
結論
延伸閲讀…
特殊直角三角形- 維基百科,自由的百科全書
三邊為345的直角三角形的內角度數
3 4 5 三角形之角度特性具有重要的數學和物理意義。透過瞭解其角度關係、畢氏定理、三角函數和實際應用,我們可以更深入地瞭解三角形並解決實際問題。
