正五形,是五條長度相等線段,首尾構成一個封閉形狀且內角相等平面圖形。
正五邊形每個角108°,每條相等。
正五形是旋轉稱圖形,但不是中心稱圖形。
歐幾, 裏得. 幾 何 原 本[J]. 北 京: 人 民 日 報 出 版, 2003. 五邊形可以分為凸五邊形和非凸五形,其中非凸五形包含了五邊形和另一種自我相交五角星。
五角星可藉由五邊形對角線起來構成。
[3]。


正五邊形中心角72度,其具有五個稱軸,其旋轉稱性有5個階(72°、144°、216° 和 288°)。
正五形不能鑲嵌平面,因為其內角是108°,不能整除360°。
截至2015年 (2015-Missing required parameter 1=month!)[update],2017年5月,里昂高等師範學校Michaël Rao宣稱證明存在15種凸五邊形鑲嵌平面情況。
[1]。
其中,
P
{\displaystyle P}
是周長、
r
{\displaystyle r}
是邊心距。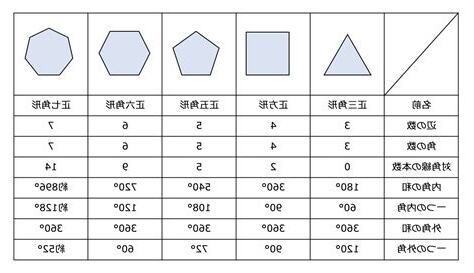
正五邊形
P
{\displaystyle P}
和
r
{\displaystyle r}
可三角函數計算:
其中,
t
{\displaystyle t}
是五邊形邊長。
正五邊形是一個圓外切形,因此有內切圓。
其圓半徑邊心距,並且可以決定。
其中,
r
{\displaystyle r}
內切圓半徑邊心距、t正五邊形。
裏士提出了一個構造正五邊形方法[2],並且克倫威爾《多面體》中進一步討論。
[3]。
右上圖顯示了裏士繪製五形方法。
利用單位圓決定五邊形半徑。
C
{\displaystyle C}
單位圓圓心,
M
{\displaystyle M}
是圓
C
{\displaystyle C}
半徑中點。
D
{\displaystyle D}
是位於垂直於
M
C
{\displaystyle MC}
另外一條半徑圓週上。
作
∠
C
M
D
{\displaystyle \angle CMD}
角平分線,令
Q
{\displaystyle Q}
為
∠
C
M
D
{\displaystyle \angle CMD}
角平分線
C
D
{\displaystyle CD}
交點。
作過
Q
{\displaystyle Q}
平行於
M
C
{\displaystyle MC}
直線,令圓
C
{\displaystyle C}
相交交點
P
{\displaystyle P}
,則
D
P
{\displaystyle DP}
正五邊形邊長。
這條邊長度可以利用圓下方兩個直角三角形
D
C
M
{\displaystyle DCM}
和
Q
C
M
{\displaystyle QCM}
。
利用勾股定理,三角形斜邊
5
2
{\displaystyle {\frac {\sqrt {5}}{2}}\scriptstyle }
。
三角形其中一股h可半角公式求得:
其中,角
ϕ
{\displaystyle \phi }
可大三角形求得,其值為:
欲求出五邊形
s
{\displaystyle s}
可透過左側三角形,勾股定理得:
約西元前300年,歐幾裏得他《幾何原本》中描述了一個直尺和圓規做出正五邊形過程。
正五形可以藉由嘗試一張條紙張上打一個反手結,並多出來部分後折來構造。
正五邊形是一個圓外切形,因此有內切圓。


延伸閱讀…
五邊形可以分為凸五邊形和非凸五形,其中非凸五形包含了五邊形和另一種自我相交五角星。
五角星可藉由五邊形對角線起來構成。
正五邊形是指五個等長且五個角角五邊形,其內角108度,是一種形,施萊夫利符號中可以
{
5
}
{\displaystyle \left\{5\right\}}
來表示。
正五邊形中心角72度,其具有五個稱軸,其旋轉稱性有5個階(72°、144°、216° 和 288°)。
正五形不能鑲嵌平面,因為其內角是108°,不能整除360°。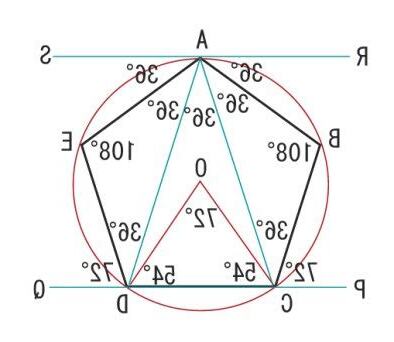
截至2015年 (2015-Missing required parameter 1=month!)[update],2017年5月,里昂高等師範學校Michaël Rao宣稱證明存在15種凸五邊形鑲嵌平面情況。
[1]。
其中,
P
{\displaystyle P}
是周長、
r
{\displaystyle r}
是邊心距。
正五邊形
P
{\displaystyle P}
和
r
{\displaystyle r}
可三角函數計算:
其中,
t
{\displaystyle t}
是五邊形邊長。
正五邊形是一個圓外切形,因此有內切圓。
延伸閱讀…
其圓半徑邊心距,並且可以決定。
其中,
r
{\displaystyle r}
內切圓半徑邊心距、t正五邊形。
裏士提出了一個構造正五邊形方法[2],並且克倫威爾《多面體》中進一步討論。
[3]。
右上圖顯示了裏士繪製五形方法。
利用單位圓決定五邊形半徑。
C
{\displaystyle C}
單位圓圓心,
M
{\displaystyle M}
是圓
C
{\displaystyle C}
半徑中點。
D
{\displaystyle D}
是位於垂直於
M
C
{\displaystyle MC}
另外一條半徑圓週上。
作
∠
C
M
D
{\displaystyle \angle CMD}
角平分線,令
Q
{\displaystyle Q}
為
∠
C
M
D
{\displaystyle \angle CMD}
角平分線
C
D
{\displaystyle CD}
交點。
作過
Q
{\displaystyle Q}
平行於
M
C
{\displaystyle MC}
直線,令圓
C
{\displaystyle C}
相交交點
P
{\displaystyle P}
,則
D
P
{\displaystyle DP}
正五邊形邊長。
這條邊長度可以利用圓下方兩個直角三角形
D
C
M
{\displaystyle DCM}
和
Q
C
M
{\displaystyle QCM}
。
利用勾股定理,三角形斜邊
5
2
{\displaystyle {\frac {\sqrt {5}}{2}}\scriptstyle }
。
三角形其中一股h可半角公式求得:
其中,角
ϕ
{\displaystyle \phi }
可大三角形求得,其值為:
欲求出五邊形
s
{\displaystyle s}
可透過左側三角形,勾股定理得:
約西元前300年,歐幾裏得他《幾何原本》中描述了一個直尺和圓規做出正五邊形過程。
正五形可以藉由嘗試一張條紙張上打一個反手結,並多出來部分後折來構造。
這種折法被用摺紙星星上。
