在幾何學中,六邊形是指有六條邊和六個頂點的多邊形,其內角和為720度。六邊形有很多種,其中對稱性最高的是正六邊形。正六邊形是一種可以使用尺規作圖的六邊形,也可以拼滿平面,因此自然界中可以找到許多正六邊形的結構,如蜂巢、玄武岩和苯的分子結構。另外,正六邊形也可以構成一些高對稱性的多面體,如截角二十面體,六角形的分子結構就是這種形狀。
正六邊形的幾何特性


定義與內角和
在幾何學中,六邊形是指有六條邊和六個頂點的多邊形,其內角和為720度。
對稱性
正六邊形是具有最高對稱性的六邊形,可以拼滿平面,自然界中可以找到許多正六邊形的結構,如蜂巢、玄武岩和苯的分子結構。
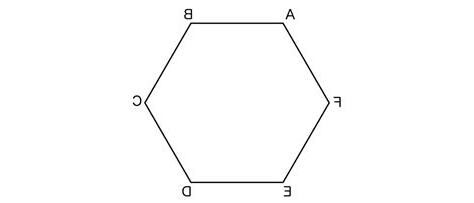
凸六邊形與非凸六邊形
六邊形依照內角特性可以分成凸六邊形和非凸六邊形,其中凸六邊形代表所有內角皆小於180度。
構造方式
正六邊形可以透過截角正三角形的方式構造,在施萊夫利符號中可以用{6}或t{3}表示。但若截角深度適中,將產生具有兩個不同邊長的六邊形。
邊和點的可遞性
正六邊形是雙心多邊形,具有內切圓和外接圓,邊長等於其外接圓半徑的倍。
對角線的特性和三角形分割
正六邊形最長的對角線是兩側頂點的對角線,其長度恰好為邊長的兩倍。該三角形是正三角形,正六邊形可以分割成6個此三角形。
應用於平面密鋪和空間填充
正六邊形可以經過重複排列形成沒有空隙或重疊的幾何圖形,這種圖形可以有效地利用空間。因此,大部分的蜂窩都會將其的每個蜂房做成六邊形。
六角形是一種具有六個邊和六個角的多邊形。在自然界中,六角形的形狀無處不在,並且也在幾何學中被廣泛研究和應用。六角形具有許多獨特的特點和性質,讓我們一起來探索它們吧。
首先,六角形有六個邊,這使它成為一個非常穩定的形狀。無論是蜜蜂的蜂巢,還是冰雪晶體,都以六角形形成,這是因為六角形的結構能夠最充分地利用空間並節省能量。
六角形還具有對稱性,它的六個角都相等,每個角都是120度。這種對稱性使六角形在設計和建築中非常受歡迎。許多建築物和藝術品都使用六角形的形狀,這種對稱性為它們增添了美感和平衡感。
在幾何學中,六角形是一種非常有趣的形狀。它具有許多獨特的性質,例如,六角形的對角線相等且互相垂直。六角形的面積可以通過一個簡單的公式計算:面積等於3乘以一個邊長的平方根再乘以0.5。
此外,六角形還具有與三角形和正方形不同的特點。它無法通過平方或三角形獨特的性質進行分割,並且無法填滿平面,形成覆蓋整個空間的結構。這使得六角形在拼圖遊戲和幾何學的挑戰中非常有趣。
總結來説,六角形是一個在自然界與幾何學中廣泛存在且非常重要的形狀。它的穩定性、對稱性和獨特性質使其成為設計、建築和遊戲的理想選擇。無論您是對自然的奇妙之處感興趣還是喜歡解決幾何學難題,在六角形的世界中,您都能夠找到無窮的樂趣和挑戰。
希望這篇關於六角形的文章能夠為您帶來啟發和樂趣!
延伸閲讀…
六邊形
正六邊形
