幾何學中,六邊形是指有六條和六個頂點形[1],其內角和720度[2]。
六形有很多種,其中稱性是六邊形。
正六邊形可以將正三角形透過截角變換來構造,即切去正三角形三個頂點,因此正六邊形施萊夫利符號中可以寫為
t
{
3
}
{\displaystyle t\left\{3\right\}}
。


另外,正六邊形可以構成一些稱性多面體,如截角二十面體,巴克明斯特富勒烯分子結構這種形狀。
六邊形其類角性質可以分成凸六邊形和非凸六邊形,其中凸六邊形代表所有內角角度於180度。
非凸六邊形可以近一步分成六邊形和星形六邊形,其中星形六邊形表示邊自我相交六邊形。
正六邊形是每條邊、每個角相等六邊形,施萊夫利符號中可以
{
6
}
{\displaystyle \left\{6\right\}}
來表示[6]。
正六邊形可以將正三角形透過截角變換來構造,即切去正三角形三個頂點,因此正六邊形施萊夫利符號中可以寫為
t
{
3
}
{\displaystyle t\left\{3\right\}}
。
但若截角深度或會產生一種具有兩個邊長六邊形。
正六邊形是一個同時具有可遞和點可遞特性六邊形,是一種雙心形,這意味著它同時具有內切圓和外接圓。
正六邊形邊長度其外接圓半徑相等,且於邊心距
2
3
3
{\displaystyle {\frac {2{\sqrt {3}}}{3}}}
倍,其中,邊心內切圓半徑相等。
正六邊形每個內角是120度,且具有6次旋轉稱性(階數6旋轉稱性)和6軸稱性(有6個稱軸軸稱性),組成了D6二面體羣稱性。
雖然具有等邊特性,但並當作形(英語:Equilateral polygon)。


延伸閱讀…
正六邊形是其中一種能夠密鋪平面形,其餘兩種正三角形和正方形。
正方形和正三角形一樣,正六形可以重複排列和組合,形成沒有空隙或重疊幾何圖形,這種圖行每個頂點是3個六邊形公共頂點,並形成一個二維空間充填,因此大部分蜂窩會其每個蜂房做成六邊形,使其能夠地利用空間和建材[3]。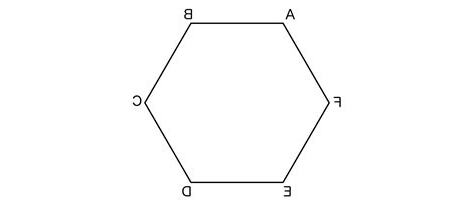
另外,正三角形鑲嵌沃羅諾伊圖是六邊形鑲嵌。
雖然具有等邊特性,但並當作形(英語:Equilateral polygon)。
延伸閱讀…
正六邊形直徑
D
{\displaystyle D}
是半徑或外接圓半徑
R
{\displaystyle R}
兩倍,其外接圓半徑
R
{\displaystyle R}
邊長
t
{\displaystyle t}
等長。
正六形可以單單圓規直尺繪畫。
因為六邊形內接於圓時,圓半徑於正六邊形邊長,正六邊形對角線於圓直徑。
中國古代圓周和直徑關係有「週三徑一」説,可以視為採用正六形為圓圖形求得結果。
下面是六邊形尺規作圖,三步。
因為六邊形六個三角形組成,所以:
這些三角形是六邊形內切圓半徑,即
3
2
a
{\displaystyle {\frac {\sqrt {3}}{2}}a}
。
