【凸意思】她疑惑被顧客傳 |她收1表情符號錯愕 |在線漢字編碼查詢 |

凸集

與仿射集相關的另一個重要概念是凸集。一個集合 C 被稱為凸集，當且僅當對任意兩點 \( x_1, x_2 \) 屬於 C，所有介於這兩點的線段也都屬於 C。凸集是一種極為普遍的幾何結構，它們在微積分、最優化理論和控制理論中都有著廣泛應用。在 \( R^n \) 中，所有的線段、凸多邊形乃至於更高維度的超凸體都是凸集。

從定義中，我們可以看出優化問題有幾個關鍵要素：

• 可行解的集合
• 目標函數的形式
• 目標函數的極值點

凸優化的定義

凸優化問題只考慮可行解為凸集且目標函數為凸函數的情況。在下一章節中，我們將介紹凸集的概念。

仿射集的概念

一個集合C是仿射集，當且僅當對於任意\

仿射集與凸集的性質

在研究幾何對象的性質時，尤其是在高維空間中，仿射集和凸集的概念扮演著重要的角色。以下是一篇對於這些概念的解釋和應用的小文章。

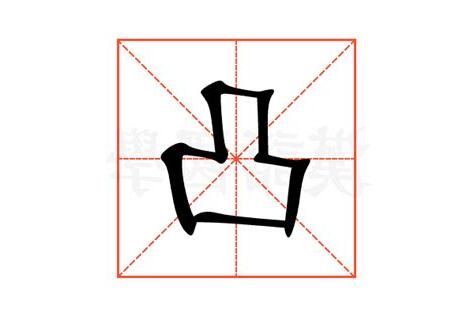
• 仿射集

  設有一個包含於歐幾裏得空間中的集合 C，我們説 C 是仿射集當且僅當，對於 C 內任意兩點 \( x_1, x_2 \)，連接這兩點的直線的每一點也都屬於 C。這種特性使得仿射集在幾何上非常自然，因為它們代表了空間中的平坦部分。在實數空間 \( R^n \) 中，所有的直線、平面乃至於更高維度的超平面都是仿射集。

• 凸集

  與仿射集相關的另一個重要概念是凸集。一個集合 C 被稱為凸集，當且僅當對任意兩點 \( x_1, x_2 \) 屬於 C，所有介於這兩點的線段也都屬於 C。凸集是一種極為普遍的幾何結構，它們在微積分、最優化理論和控制理論中都有著廣泛應用。在 \( R^n \) 中，所有的線段、凸多邊形乃至於更高維度的超凸體都是凸集。

• 仿射包

  給定一個點集，我們可以定義一個包含這些點的最小仿射集，這一最小仿射集被稱為這些點的仿射包。仿射包的概念允許我們從給定的點集抽取本質幾何結構，並且對於理解這些點在何種程度上代表了空間的某一維度有著重要意義。

• 直線方程與線段

  直線方程 \( y = \theta x_1 + (1 – \theta) x_2 \) 描述了從點 \( x_1 \) 到點 \( x_2 \) 的整條直線。當 \( \theta \) 取值於區間 \( [0, 1] \)

  凸集與仿射集的區別

  在幾何學中，凸集和仿射集是兩種不同的集合類型，它們在維度不高的空間中容易區分，但在高維空間中可能較難 visualization。簡單來説，凸集是這樣一個區域，其中任意兩點的直線連線仍然在集合內。而仿射集則是更加限制性的類型，它們是通過線性變換生成的新集合，這些線性變換保持了原始集合的某些特徵。

  為了更深入地理解這兩種集合的區別，我們可以看一個簡單的例子。在一個維度為一（即一維線性空間）的空間中，任意一條直線本身都是凸集，因為兩點之間的任何線段都在這條直線上。然而，只有當這條直線是通過線性變換從原始集合映射而來時，它才成為一個仿射集。例如，將一個實數軸上的閉合區間映射到同一直線上的其他部分，會得到一個仿射集，因為這個映射是一個線性變換。

  

  在高維空間中，凸集和仿射集的區別可能不太明顯。一個集合可能既是凸集又是仿射集，但如果它不是仿射集，那麼它就不可能是凸集。這一點可以從凸集的定義中看出：對於任意兩個點 x1 和 x2 在集合 C 中，以及任意 \theta 介於 0 和 1 之間，\theta x1 + (1 – \theta)x2 也必須在集合 C 中。這意味著任何包含在集合 C 中的直線段也必須在集合 C 內。

  • 仿射集（Affine Set）：當可行域為n維空間中的任意一個n維仿射集時，意味著每一個n維特徵向量都是合乎要求的解。這意味著在合適的n維特徵結構中表示下，數據集可以在所有維度上自由變化。

    

    延伸閲讀…

    她疑惑被顧客傳「凸^

    【凸】在線漢字字典、在線漢字意思查詢、在線漢字編碼查詢【鄭碼、五筆編碼、倉頡碼】

    定義：若 x_1,…,x_k \in C, \theta _1, …, \theta _k \ge 0 ，則 \theta_1x_1+…+\theta _kx_k 為一個凸錐組合。

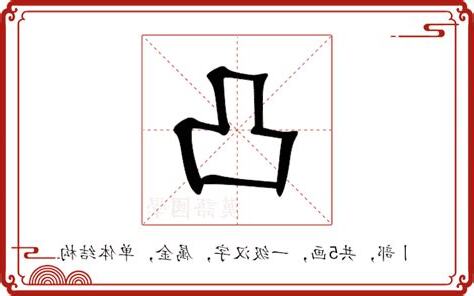
    定義：包含 x_1, …, x_k 的最凸錐集即為凸錐包。 意義與仿射包類似，這裏不多説。仿射集是兩點的直線（或多個點的所有可能直線）仍在集合中，凸集是兩點的線段（或多個 可視化理解可行域 在優化問題中，我們常常遇到對象函數 f(x) 在特定約束條件下的極值問題。這些約束條件定義了一個可行解的集合，即所謂的可行域。為了更好地理解這些概念，這裡我們進行一些簡要的總結。 仿射集（Affine Set）：當可行域為n維空間中的任意一個n維仿射集時，意味著每一個n維特徵向量都是合乎要求的解。這意味著在合適的n維特徵結構中表示下，數據集可以在所有維度上自由變化。 延伸閲讀… 她收1表情符號錯愕「在罵我？」 網勸別亂用：超失禮 凸優化學習筆記 凸集（Convex Set）：一個集合被稱為凸集，當其滿足對於任意兩點之間的線段上的所有點，也屬於該集合。這意味著從集合內的兩點連接而成的線段仍保持在集合內。 凸錐（Convex Cone）：一個集合被稱為凸錐，當其滿足對於任何一組向量，這些向量的非零線性組合仍屬於該集合。這意味著由這些向量所夾的區域內的任意點都是可行的。 關係總覽：凸集是凸錐的子集，而仿射集則是凸集的子集。因此，凡是仿射集，必然也是凸集。 示例凸集：所有n維空間本身既是仿射集，也是凸集。子空間（Subspace）是一個滿足特定條件（線性閉合性）的集合，它們都是 倒序改寫的文章 令 \left[ \theta_0,\theta_1,…,\theta_k \right]=y ，則 y\geq 0, I^Ty \leq1 。其中 B=[v_1-v_0,…,v_k-v_0] \in R^{n \times k} 。若 Rank(B)=k ，則可通過行列變換將B化為 \begin{bmatrix} I_k \\ 0 \end{bmatrix}_{n \times k} ，其中 I_k \in R^{k \times k} 。也即存在非奇異矩陣 A= \begin{bmatrix} A_1 \\ A_2 \end{bmatrix} \in R^{n \times n} ，使得 AB=\begin{bmatrix} A_1 \\ A_2 \end{bmatrix}B=\begin{bmatrix} I_k \\ 0 \end{bmatrix} 。\Leftrightarrow\left\{\begin{matrix} \begin{align} A_1x&=A_1v_0 + y\\ A_2x&=A_2v_0 \end{align} \end{matrix}\right. ，其中 0 \leq y \leq I^T 。可表示為超平面與半空間的交集，因此單純形為多面體。實際上 S^n 是凸錐，凸錐必是凸集。證明： \forall \theta_1,\theta_2 \ge 0,x_1,x_2 \in C 。可以看到此時的 x 不再是向量而是矩陣形式，這就更難想象出它的可行解集合長什麼樣。（11）對稱半正定矩陣集合 S^n_{+}=\left\{ x \in R^{n \times m}| x=x^T, x\succeq0\right\} 。x\succeq0 表示矩陣x的特徵值大於等於0，而不是x本身大於等於0。\forall \theta_1,\theta_2 \ge 0, \forall A, B \in S^n_+ ，只需證明 \theta_1A+\theta_2 半正定二次型的性質 性質 條件 證明 x^T(\theta_1A+\theta_2B)x \ge 0 \forall \theta_1,\theta_2 \ge 0, \forall A, B \in S^n_{++} x^TAx > 0, x^TBx > 0, 但 x^T(\theta_1A+\theta_2B)x \ge 0 凸集的定義如下： 集合 S \subset R^n 為凸集，當且僅當對任意兩點 x, y \in S ，連線段 \overline{xy} \subset S。 保凸運算包括： 集合的交集：若 S_1,S_2 為凸集，則 S_1\cap S_2 為凸集。 多個凸集的交聯：若 S_a 為凸集， \forall a \in A ，則 \bigcap_{a \in A}^{Sa} 為凸集。 仿射函數的預像：若 S \subset R^n 是凸集， f:R^n->R^m 是仿射函數，則 f(S) = \left\{ f(x)|x \in S \right\} 為凸集。 例如，橢球 \varepsilon 和單位球 \left\{ u| \ \ ||u||_ 2 \le 1\right\} 都是凸集。橢球的方程為 \( (x-x_c)^TP^{-1}(x-x_c) \le 1 \)，其中 P \in S^n_{++}。 作仿射變換 f(u)=P^{\frac{1}{2}}u+x_c 定義 x=P^{\frac{1}{2}}u+x_c 則 u=P^{-\frac{1}{2}}(x-x_c) g:R^k->R^n 為仿射，則稱 g^{-1}\left\{ x|g(x ) \in S \right\>為逆映射。 即若 S 為凸集，則 \alpha S=\left\{ \alpha x| x\in S \right\>, S+a=\left\{ x+a| x\in S \right\> 均為凸集。